Санкт-Петербургский государственный университет информационных технологий,

механики и оптики

Построение зубьев методом огибания

Методические указания

к выполнению лабораторной работы

Санкт-Петербург

2008

Содержание

1. Краткие сведения об образовании эвольвентных профилей зубьев методом обкатки 3

2. Оборудование и приборы 8

3. Описание прибора 8

4. Порядок выполнения работы 11

5. Содержание отчёта 14

6. Вопросы для тестов 16

7. Таблица значений эвольвентного угла invα 20

Литература 24

1. Краткие сведения об образовании эвольвентных профилей зубьев методом обкатки

Цель работы - ознакомить с наиболее распространенным методом образования зубьев цилиндрических прямозубых колёс, а также с явлением подрезания зубьев в процессе их изготовления и с контролем точности изготовления зубчатого венца.

При изготовлении зубчатых колёс методом обкатки (огибания) режущий инструмент может иметь форму зубчатого колеса. Во время нарезания зубьев инструменту и заготовке сообщают такие движения, которые имели бы соответствующие им зубчатые колеса в зацеплении. Тот же метод применяется и в случае использования инструмента, имеющего форму зубчатой рейки. При нарезании зубьев прямозубого колеса 1 производящей зубчатой рейкой 2 (рис. 1) его делительную окружность 3 делают центроидой в относительном движении инструмента и заготовки. Для этого соотношение между скоростью V рейки и угловой скоростью ω нарезаемого колеса устанавливают таким, чтобы:

;

здесь d – диаметр делительной окружности, определяемый из выражения:

, (1)

где z – число зубьев нарезаемого колеса; m – модуль зубчатой рейки и нарезаемого колеса.

Центроидой ("начальной прямой") 4 рейки служит прямая, параллельная скорости перемещения рейки и касающаяся делительной окружности колёса.

Положение начальной прямой на рейке определяют расстоянием xm от делительной прямой 5 рейки до делительной окружности колеса. Одновременно это расстояние характеризует взаимное положение рейки и заготовки. Величину xm называют абсолютным сдвигом или смещением исходного контура (рейки), а величину x – относительным сдвигом или коэффициентом смещения. Смещение считают положительным x>0, если делительная прямая рейки проходит вне делительной окружности колеса.

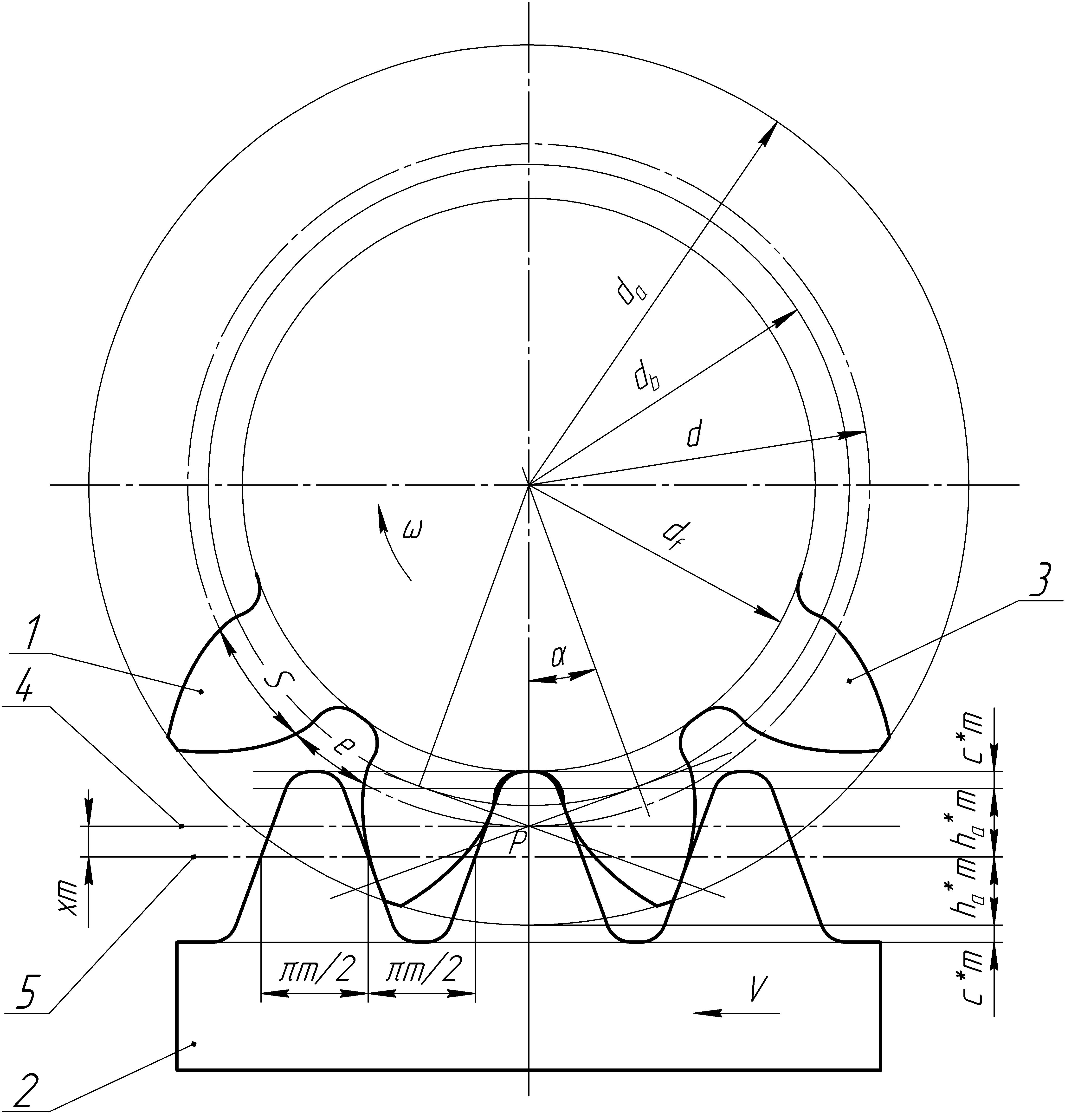
Рис. 1

Нарезание зубчатых колёс с различными по величине смещениями позволяет получать различные качественные показатели зацепления.

Если сумма коэффициентов смещения в рабочем зацеплении положительна , то такое зацепление называют положительным, соответственно даёт отрицательное зацепление, a – нулевое зацепление. В свою очередь нулевое зацепление образуется либо при и , либо при (нулевое равносмещённое зацепление).

Отдельно взятое зубчатое колесо в зависимости от знака смещения также называют положительным ( ), отрицательным ( ) или нулевым ( ).

Приведём основные геометрические' соотношения между размерами зубчатого колеса.

Диаметр основной окружности:

; (2)

Диаметр окружности впадин, образуемый вершинами зубьев рейки:

; (3)

Диаметр окружности вершин зубьев (диаметр заготовки колеса), определяемый из условия необходимой величины радиального зазора с^* в рабочем зацеплении:

; (4)

В выражениях (2), (3), (4) величины , , являются параметрами исходного контура, стандартные величины, для которых установлены (для ) ГОСТ 13755-81: , при этом – коэффициент уравнительного смещения, зависящий от и , т.е. от коэффициентов смещения, использованных при нарезании обоих колес пары.

Так как в рамках данной работы никаких сведений о втором колесе зубчатой пары не имеется, будем считать, зацепление нулевым, т.е. , а в этом случае и .

Толщина зуба s и ширина впадины e по дуге делительной окружности:

; (5)

; (6)

Для упрощения измерения делительной толщины зуба (ширины впадины) можно измерить величину делительной, хорды зуба (хорда впадины ) и пересчитать их в соответствующие величины дуг по следующим формулам:

; (5а)

; (6а)

Коэффициенты смещения x назначают в зависимости от требований, которым должны удовлетворять нарезаемые колёса. Так для получения колёс без подрезания их зубьев необходимо, чтобы:

; (7)

где x_min – значение коэффициента смещения, определяющее граничное состояние по подрезанию. При подрезание отсутствует.

С учётом стандартных значений и выражение (7) можно представить в виде:

; (8)

Из выражения (8) видно, что для стандартных значений параметров исходного контура число зубьев нарезаемого прямозубого колеса, граничное по подрезанию z_min, равно 17. При и происходит подрезание.

Среди способов контроля точности изготовления эвольвентных зубчатых колёс (особенно мелкомодульных с m<1) большое распространение имеет контроль размера по роликам.

Для контроля этого размера во впадины, между зубьями вкладываются ролики диаметром D (как доказано на рис. 2) и с помощью микрометра или штангенинструмента измеряют размер М. Центр ролика диаметра D находится на расстоянии r_p от оси колеса. Эвольвента», проведённая через центр ролика, имеет в этой точке угол развёрнутости и соответствующий ему полярный угол определяемый выражением:

; (9)

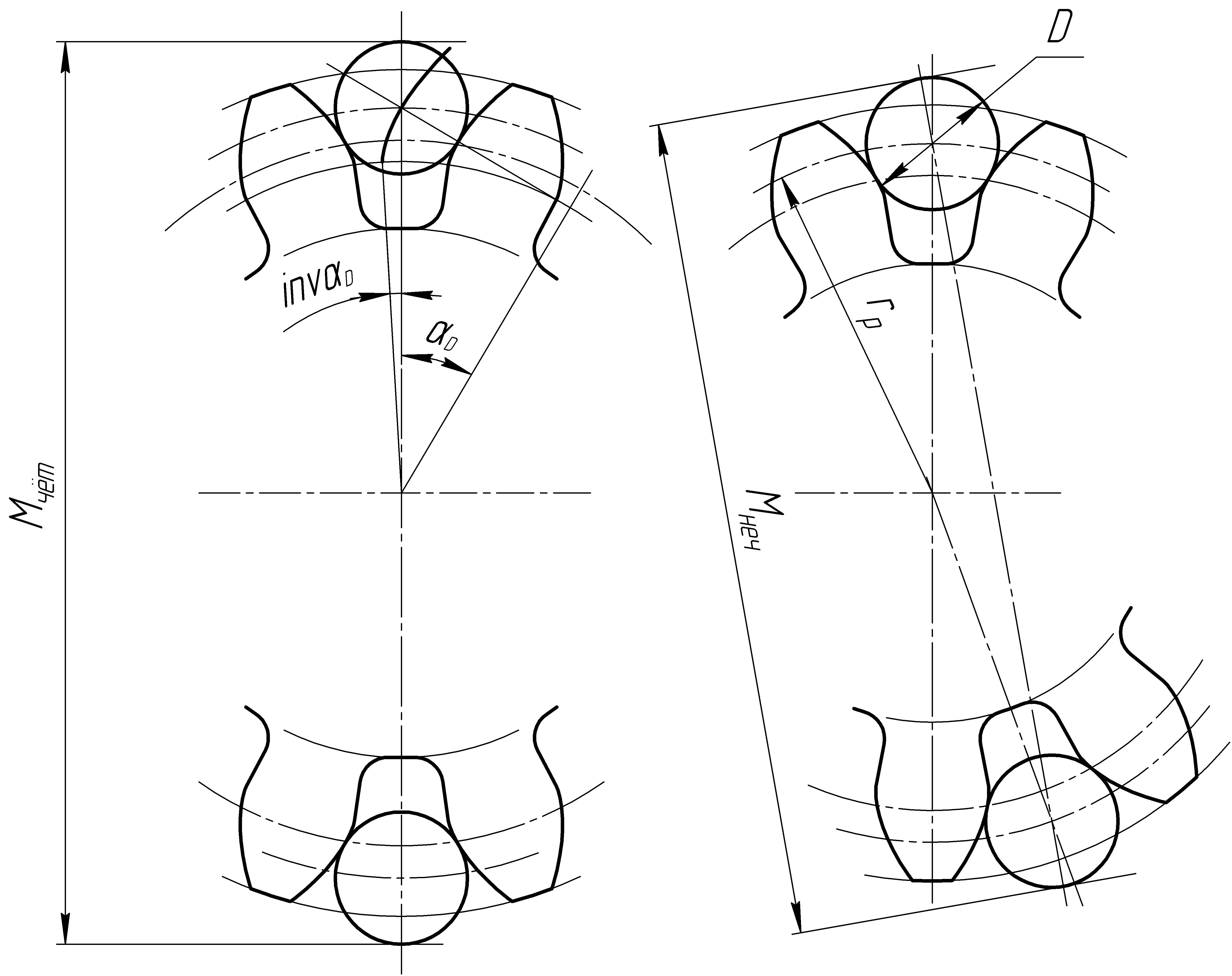
Для колёс с чётным z Для колёс с нечётным z

Рис. 2

Расстояние r_p от оси колеса до центра ролика:

; (10)

Размеры по роликам M соответственно для чётного и нечётного числа зубьев (рис. 2) рассчитываются по формулам:

; (11)

; (12)

Зависимость погрешности толщины зуба по дуге делительной окружности от отклонения положения центра ролика Δr_p:

; (13)

причём

, (14)

где r_рд – положение центра ролика, полученное в результате измерения; r_p – теоретическое положение центра ролика, полученное из выражения (10).