32.СЛОЖЕНИЕ КОЛЕБАНИЙ:

Колебания могут складываться и при этом усиливать или гасить друг друга, или изменять траекторию движения тела. Рассмотрим сложение колебаний, совершаемых в одном направлении. Пусть осциллятор совершает два одновременных колебания в одном направлении и одинаковой частоты ω₀:

x₁=A₁cos(ω₀t+₁) и x₂=A₂cos(ω₀t+₂).

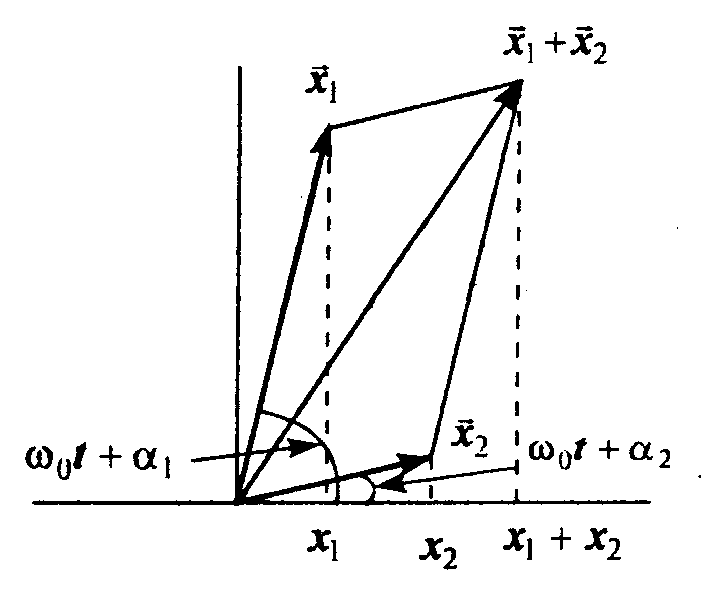
При этом суммарное колебание координаты x(t) равно x = x₁ + x₂. Представим колебания x₁ и x₂ в виде векторов на плоскости (рис.), модулями которых являются амплитуды колебаний, а фазы колебаний будут служить углами наклона векторов к оси x. При изменении времени векторы x₁ и x₂, будут равномерно вращаться в плоскости рисунка, однако разность фаз между колебаниями остается неизменной. Из рисунка видно, что вектор x = x₁ + x₂, представляет собой сумму колебаний x₁ и x₂. В самом деле, проекции векторов x₁, и x₂, на ось x соответственно равны A₁cos(ω₀t+₁) и А₂cos(ω₀t+₂), а проекция вектора x равна сумме этих проекций. Результирующее колебание также можно записать в виде: x(t)=x₁+x₂= = Acos(ω₀t+). Частота результирующего колебания равна частоте складываемых колебаний, т. е. результирующее колебание также гармоническое. Амплитуду результирующего колебания нетрудно найти из рис.

, (3.15)

а новую начальную фазу определить так:

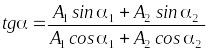. (3.16)

Из формулы (3.15) следует, что амплитуда результирующего колебания существенно зависит от значения разности фаз начальных колебаний. Если разность фаз ₁–₂=0, колебания находятся в фазе, и амплитуды A₁ и A₂ складываются A = A₁ + A₂. Если же разность фаз равна ±, колебания находятся в противофазе, т.е. амплитуда результирующего колебания A = |A₁ – A₂|.

Выше было рассмотрено сложение двух колебаний с одинаковой частотой, при этом результирующее колебание осталось гармоническим с той же частотой. Если складываются колебания разной частоты, то векторы x₁ и x₂ в плоскости будут вращаться с разной скоростью (рис.). Тогда результирующий вектор в процессе вращения будет изменяться по величине и описывать сложное негармоническое колебание.

Рассмотрим сложение колебаний во взаимно перпендикулярных направлениях. Наиболее простым примером такого колебания являются одновременные колебания частицы в направлениях x и y, происходящие с одинаковыми частотами и амплитудами (см. формулы (3.11)). Как было установлено, результирующее движение представляет собой равномерное вращение в плоскости по окружности с радиусом, равным амплитудам колебаний величин x и y. В случае неравных амплитуд и частот элементарных колебаний результирующее движение может происходить по весьма сложным траекториям и не будет гармоническим.

Таким образом, сложение гармонических колебаний с различными частотами и амплитудами позволяет осуществить колебание произвольной формы. Это обстоятельство используется для создания негармонических колебаний необходимой формы. Отсюда следует и обратное утверждение: всякое сложное негармоническое колебание может быть представлено в виде суммы простых гармонических колебаний. Другими словами, движение сложной колебательной системы со многими степенями свободы можно описать, рассматривая соответствующий набор гармонических осцилляторов.

Свободные механические колебания могут существовать в системах, где сохраняется полная механическая энергия. В реальных системах всегда присутствует трение, благодаря которому свободные колебания, возбужденные первоначально в системе, со временем будут затухать. Кроме того, колебания в различных системах часто происходят под действием внешней силы — так называемой вынуждающей силы. Колебания при наличии сил трения являются затухающими, а под действием внешней силы — вынужденными.

ГАРМОНИЧЕСКИЙ АНАЛИЗ:

Кратко: Гармонический анализ, отдел математики, связанный с разложением колебаний на гармонические колебания. При изучении периодических (т. е. повторяющихся во времени) явлений рассматриваются периодические функции.

название раздела математики и математич. метода. В Г. а. как раздел математики обычно включают: теорию тригонометрических рядов (одномерных и многомерных), Фурье преобразований (функций одного и нескольких переменных), почти периодических функций, Дирихле рядов, приближения теорию (функций тригонометрическими полиномами), гармонический анализ абстрактный и нек-рые другие математич. дисциплины, близкие к указанным. Метод заключается в сведении нек-рых задач (из различных областей математики) к вопросам Г. а. и решаемых на его основе. Напр.: теория функций комплексного переменного в вопросах граничного поведения аналитических в единичном круге функций, по существу, сливается с теорией тригонометрич. рядов; изучение свойств случайных величин при помощи харак-теристич. функций - применение метода Г. а. в теории вероятностей; нек-рые объекты функционального анализа тесно связаны с тригонометрич. рядами, почти периодич. функциями и др. объектами Г. а.; в теории дифференциальных уравнений при помощи относящегося к Г. а. Фурье метода находятся решения различных уравнений математич. физики; наконец, многочисленные прикладные задачи вычислительной математики решаются на основе применения рядов и интегралов Фурье - объектов

33. Диагностическое применение гармонических колебаний:

Сложение гармонических колебаний, направленных по одной прямой. Возможны случаи, когда тело участвует одновременно в нескольких колебаниях, происходящих вдоль одного и того же или вдоль различных направлений. Рассмотрим сложение двух гармонических колебаний одинакового направления, одинаковой частоты и с одинаковыми амплитудами, но с разными начальными фазами a₀₁ и a₀₂ . Смещение x колеблющегося тела будет суммой смещений x₁и x₂: x = x₁ + x₂ = Acos(w₀t + a₀₁) + Acos(w₀t + a₀₂). Используя известную из тригонометрии формулу для суммы косинусов двух углов,   имеем: A_рез  ,  то есть получается гармоническое колебание той же частоты с начальной фазой   и амплитудой A_рез . Как видно, амплитуда A_резрезультирующего колебания зависит от разности фаз складываемых колебаний. Рассмотрим два крайних случая: А) Колебания происходят в фазе, то есть a₀₁ = a₀₂, тогда   и  , поэтому A_рез = 2A. Если амплитуды не равны, A_рез = A₁ + A₂

Б) Колебания происходят в противофазе, то есть a₀₁ = a₀₂ ± p, тогда  . Следовательно, и A_рез = 0. Если амплитуды не равны, например, A₁ > A₂ , тоA_рез = A₁ - A₂. Таким образом, при сложении двух одинаково направленных гармонических колебаний одного периода и с равными амплитудами получается гармоническое колебание того же периода с амплитудой, которая в зависимости от соотношения фаз складываемых колебаний может изменяться от удвоенного значения, если колебания происходят в фазе, до нуля, если они находятся в противофазе. При сложении гармонических колебаний с разными частотами результирующее колебание не будет гармоническим, а будет являться сложным колебанием (

Рис. 4. Сложение гармонических колебаний с разными частотами: А) исходные колебания, Б) результирующее колебание. Сложное колебание и его гармонический спектр. Согласно теореме Фурье, любое сложное колебание может быть представлено как сумма простых (гармонических) колебаний (гармоник), периоды или частоты которых кратны основному периоду или частоте сложного колебания. Совокупность простых колебаний, на которые можно разложить данное сложное колебание, называется его гармоническим спектром. В гармоническом спектре сложного колебания указываются частоты и амплитуды всех составляющих его простых колебаний. Обычно спектр изображается в виде графика, на горизонтальной оси которого откладываются частоты; затем для каждой из частот простых колебаний имеющихся в спектре, строится ордината, соответствующая амплитуде этого колебания. Если гармонический спектр сложного колебания содержит только небольшое число простых колебаний и график его состоит из отдельных ординат, то такой спектр называется линейчатым (рис. 5.). Если спектр содержит простые колебания практически всех частот в каких-то пределах, то он называется сплошным и график его строится в виде сплошной огибающей кривой. Установление гармонического спектра является основным приемом при анализе сложного колебания. Этот анализ делается с помощью специальных приборов —гармонических анализаторов. Они применяются и в медицине при исследовании, например, колебаний биопотенциалов головного мозга и др. Многие процессы человеческого организма являются периодическими: сердечные сокращения, дыхание, кровенаполнение сосудов и т. п

				w

Сложение взаимно-перпендикулярных колебаний. В результате сложения двух взаимно-перпендикулярных колебаний различного периода тело движется по сложным фигурам, форма которых зависит от соотношения периодов, амплитуд и начальных фаз складываемых колебаний и которые называются фигурами Лиссажу. Рис. 6. Фигуры Лиссажу для колебаний различающихся начальными фазами Da.

34.ГИДРАВЛИЧЕСКОЕ СПОРОТИВЛЕНИЕ И СОГЛАСОВАНИЕ СОПРОТИВЛЕНИЙ:

ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ-

сопротивление движению жидкости, приводящее к потере механич. энергии потока (потери напора, гидравлич. потери). Г. с. подразделяют на линейные сопротивления (по длине прямолинейного трубопровода или канала), обусловл. вязкостью жидкости, и местные, возникающие в местах изменения значения или направления скорости потока (в задвижках, вентилях, кранах, коленах, тройниках, диафрагмах, диффузорах и т. д.)

СОГЛАСОВАНИЕ СОПРОТИВЛЕНИЙ(пфф, ваще ничего про это нет)

35.ФИЗИОЛОГ.И ФИЗИЧ. ХАРАКТЕРИСТИКИ ЗВУК.КОЛЕБАНИЙ:

Физические характеристики звука

Одной из важнейших характеристик звуковых волн является спектр.

• Спектром называется набор различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным.

Сплошной спектр означает, что в данном наборе присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон.

Дискретный спектр означает наличие конечного числа волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал.

По типу спектра звуки разделяются на шумы и музыкальные тона.

• Шум — совокупность множества разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т.п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр).

С развитием промышленности появилась новая проблема — борьба с шумом. Возникло даже новое понятие «шумовое загрязнение» среды обитания. Шум, особенно большой интенсивности, не просто надоедает и утомляет — он может и серьезно подорвать здоровье.

• Музыкальный тон создается периодическими колебаниями звучащего тела (камертон, струна) и представляет собой гармоническое колебание одной частоты.

С помощью музыкальных тонов создается музыкальная азбука — ноты (до, ре, ми, фа, соль, ля, си), которые позволяют воспроизводить одну и ту же мелодию на различных музыкальных инструментах.

• Музыкальный звук (созвучие) — результат наложения нескольких одновременно звучащих музыкальных тонов, из которых можно выделить основной тон, соответствующий наименьшей частоте. Основной тон называется также первой гармоникой. Все остальные тоны называются обертонами. Обертоны называются гармоническими, если частоты обертонов кратны частоте основного тона. Таким образом, музыкальный звук имеет дискретный спектр.

Любой звук, помимо частоты, характеризуется интенсивностью. Так реактивный самолет может создать звук интенсивностью порядка 10³ Вт/м², мощные усилители на концерте в закрытом помещении — до 1 Вт/м², поезд метро — около 10^–2 Вт/м².

Чтобы вызвать звуковые ощущения, волна должна обладать некоторой минимальной интенсивностью, называемой порогом слышимости. Интенсивность звуковых волн, при которой возникает ощущение давящей боли, называют порогом болевого ощущения или болевым порогом.

Интенсивность звука, улавливаемая ухом человека, лежит в широких пределах: от 10^–12 Вт/м² (порог слышимости) до 1 Вт/м² (порог болевого ощущения). Человек может слышать и более интенсивные звуки, но при этом он будет испытывать боль.

Уровень интенсивности звука L определяют по шкале, единицей которой является бел (Б) или, что гораздо чаще, децибел (дБ) (одна десятая бела). 1 Б — самый слабый звук, который воспринимает наше ухо. Эта единица названа в честь изобретателя телефона Александра Белла. Измерение уровня интенсивности в децибелах проще и поэтому принято в физике и технике.

Уровень интенсивности L любого звука в децибелах вычисляется через интенсивность звука по формуле

L=10⋅lg(II0),

где I — интенсивность данного звука, I₀ — интенсивность, соответствующая порогу слышимости.

В таблице 1 приведен уровень интенсивности различных звуков. Тем, кто при работе подвергается воздействию шума свыше 100 дБ, следует пользоваться наушниками.

Физиологические характеристики звука

Физическим характеристикам звука соответствуют определенные физиологические (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это обусловлено тем, что восприятие звука — процесс не только физический, но и физиологический. Человеческое ухо воспринимает звуковые колебания определенных частот и интенсивностей (это объективные, не зависящие от человека характеристики звука) по-разному, в зависимости от «характеристик приемника» (здесь влияют субъективные индивидуальные черты каждого человека).

Основными субъективными характеристиками звука можно считать громкость, высоту и тембр.

• Громкость (степень слышимости звука) определяется, как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1000 до 5000 Гц.

При увеличении интенсивности в 10 раз уровень громкости увеличивается на 10 дБ. Вследствие этого, звук в 50 дБ оказывается в 100 раз интенсивнее звука в 30 дБ.

• Высота звука определяется частотой звуковых колебаний, обладающих наибольшей интенсивностью в спектре.

Тембр (оттенок звука) зависит от того, сколько обертонов присоединяются к основному тону и какова их интенсивность и частота. По тембру мы легко отличаем звуки скрипки и рояля, флейты и гитары, голоса людей