3. Речной сток.
3.1. Статистические методы при гидрологических исследованиях.
В гидрологических исследованиях и расчетах расходы воды в реке являются главной характеристикой речного стока. Наряду с экстремальными значениями расходов воды (max, min) часто используются расходы воды, осредненные за различные периоды времени (сутки, месяц, сезон, год).
Порядок определения наиболее часто употребляемых гидрологических характеристик установлен нормативными документами и СНиПами.
Расход воды в реке устанавливают в зависимости от наличия или отсутствия наблюдений за водным режимом реки. При наличии ряда наблюдений устанавливаются следующие характеристики: среднее арифметическое значение расхода, среднеквадратическое отклонение, коэффициенты вариации и асимметрии.
Для вычисления среднего расхода весь ряд наблюдений разделяется на интервалы шириной
где Qmax , Qmin – максимальное и минимальное значение расходов в ряде наблюдений.
Ряд наблюдений
разделяется на число интервалов 
.
Начиная с первого значения, определяют число событий (попаданий) в полученные значения интервалов (заполняется колонка 3 нижеследующей таблице).
Для расчетов строим таблицу:
Таблица 1
Интервалы |
Середина интервала |
Число событий, m |
Эмпирическая вероятность,
|
Накопленная вероятность
|
1 |
2 |
3 |
4 |
5 |
19-17,1 |
18,05 |
2 |
6,7 |
6,7 |
17,1-15,2 |
16,15 |
2 |
6,7 |
13,4 |
15,2-13,3 |
14,25 |
7 |
23,3 |
36,7 |
13,3-11,4 |
12,35 |
9 |
30 |
66,7 |
11,4-9,5 |
10,45 |
2 |
6,7 |
73,4 |
9,5-7,6 |
8,55 |
4 |
13,3 |
86,7 |
7,6-5,7 |
6,65 |
3 |
10 |
96,7 |
5,7-3,8 |
4,75 |
1 |
3,3 |
100 |
Средне арифметическая величина статистического ряда, может быть определена по формуле:
, м3/с,
где
–
норма годового стока, 
– середина интервала.
м3/с.
Среднеквадратическое
отклонение единичных значений годового
стока
от среднего
за n лет определяется по следующей
формуле:
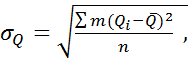
При числе лет наблюдения меньше 30 в приведенное для среднеквадратического отклонения выражение подставляется (n – 1) лет.
Мерой изменчивости той или иной величины является коэффициент Cv вариации, который представляет собой отношение среднеквадратического отклонения к среднему значению ряда:
, 
=0,28
В качестве характеристики асимметричности ряда принимается среднее значение отклонений членов ряда от его средне арифметического значения в третьей степени:
,
В симметричных распределениях отклонения от среднего взаимно уравновешиваются, поэтому равно нулю.
Коэффициент асимметрии определяют по формуле:
, 
