Напряжения

Метод сечений позволяет определить величину внутреннего си­лового фактора в сечении, но не дает возможности установить за­кон распределения внутренних сил по сечению. Для оценки прочно­сти необходимо определить величину силы, приходящуюся на любую точку поперечного сечения.

Величину интенсивности внутренних сил в точке поперечного сечения называют механическим напряжением. Напряжение харак­теризует величину внутренней силы, приходящейся на единицу пло­щади поперечного сечения.

Рассмотрим брус, к которому приложена внешняя нагрузка.

С помощью метода сечений рассечем брус поперечной плоскостью, отбросим левую часть и рассмотрим равновесие остав­шейся правой части. Выделим на секущей плоскости малую площад­ку ΔА. На этой площадке действует равнодействующая внутренних сил упругости.

Направление напряжения р_ср совпадает с направлением внутренней силы в этом сечении.

Вектор р_ср называют полным напряжени­ем. Его принято раскладывать на два вектора:

τ — лежащий в площадке сечения и σ — направленный перпендикулярно площадке.

Если вектор ρ — пространственный, то его раскладывают на три составляю­щие:

Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию.

Касательное напряжение характеризует сопротивление сечения сдвигу.

Сила N (продольная) вызывает появление нормального напря­жения σ. Силы Q_x и Q_y вызывают появление касательных напря­жений τ. Моменты изгибающие М_х и М_у вызывают появление нор­мальных напряжений σ, переменных по сечению.

Крутящий момент М_Z вызывает сдвиг сечения вокруг продоль­ной оси, поэтому появляются касательные напряжения τ.

Примеры решения задач

П оследовательность построения эпюр продольных сил

1. Изобразить расчетную схему бруса и приложить заданные силы. При необ­ходимости определить опор­ную реакцию из уравнения равновесия.

2. Брус разбить на участ­ки соответственно точкам приложения сил.

3. Определить по методу сечений продольную силу для каждого участка.

4. Найденные величины продольных сил отложить в масштабе в виде ординат, перпендикулярных оси стерж­ня. Через концы ординат провести линии; проставить знаки и заштриховать эпю­ру параллельно ординатам

П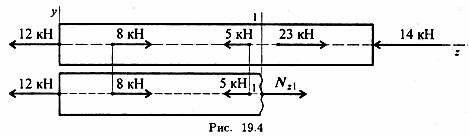 ример 1. Определить величину продольной силы в сечении 1-1 (рис. 19.4).

Решение:

Используем уравнение равновесия

Рассматривая левую часть бруса, определяем

Рассматривая правую часть бруса, определяем N_z1 = 23 — 14 = 9кН.

Величина продольной силы в сечении не зависит от того, какая часть бруса рассматривается.

Пример 3. Для бруса, изображенного на рис. 2.4, а, построить эпюру продольных сил.

Решение

Заданный брус имеет три участка 1, II, III (рис. а). Границами участков при построении эпюры N являются сечения, в которых приложены внешние силы.

1. Проведем произвольное сечение аb на участке 1 и, отбросив левую часть бруса, рассмотрим равновесие пра­вой части, изображенной отдельно на рис. 2.4, б.

2. На оставленную часть действуют сила Р₁ и искомое усилие N₁. Проектируя на ось z силы, действующие на оставленную часть, получаем:

Значение получилось со знаком плюс, что указы­вает на совпадение ее предположительного (см. рис. б) направления с действительным. Сила направлена от сечения, т. е. участок I испытывает растяжение.

3. Проведем произвольное сечение cd на участке II, от­бросим левую часть бруса и рассмотрим равновесие оставленной (правой) части, изображенной отдельно на рис. в. На оставленную часть действуют силы Р₁, Р₂ и искомое усилие N_II.. Проектируя эти силы на ось г, получаем

Сила N_II направлена от сечения, т. е. участок II испытывает растяжение.

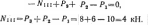4. П роведем произвольное сечение еf на участке III, от­бросим левую часть бруса и рассмотрим равновесие оставлен­ной (правой) части, изображенной отдель­но на рис. г. На оставленную часть действуют силы Р₁, Р₂, Р₃ и искомое уси­лие N_III. Проекти­руя эти силы на ось z, получаем

Сила N_III направ­лена к сечению, т. е. участок III испыты­вает сжатие.

Напомним, что продольные силы, соответствующие растяжению, принято считать положительными, а соот­ветствующие сжатию — отрицательными.

Эпюра продольных сил показана на рис. д.