7.3 Програма
%Диференціювання
%f(x)=exp(x)-sin(x) E=0.001 t=1
clc
clear all
syms x
y='exp^x-sin(x)'
d=diff(y,x)
Диференціювання в точці
%f(x)=exp(x)-sin(x) E=0.001 t=1
clc
clear all
syms x
y='exp^x-sin(x)'
d=diff(y,x)
subs(d,x,-1)
%y=exp^x-sin(x); t=-1
clc
clear all
disp('prava riznica')
del=0.001
x=-1
y1=exp(x)-sin(x)
x=-1+del
y2=exp(x)-sin(x)
diff=(y2-y1)/del
disp('liva riznica')
z=-1
a1=exp(z)-sin(z)
z=-1-del
a2=exp(z)-sin(z)
diff1=(a1-a2)/del
disp('centralna riznica')
c=-1+del/2
s1=exp(c)-sin(c)
c=-1-del/2
s2=exp(c)-sin(c)
diff2=(y2-y1)/del
7.4 Результати
y =exp^x-sin(x)
d =exp^x*log(exp)+2*x
y =exp^x-sin(x)
d =log(exp)*exp^x - cos(x)
ans =1/exp*log(exp)-2
prava riznica
del =1.0000e-003
x =-1
y1 =1.2094
x = -0.9990
y2 =1.2092
diff =-0.1727
liva riznica
z = -1
a1 = 1.2094
z = -1.0010
a2 = 1.2095
diff1 = -0.1722
centralna riznica
c = -0.9995
s1 =1.2093
c = -1.0005
s2 = 1.2094
diff2 =-0.1727
8.1 Знайти інтеграл функції, використовуючи Matlab
8.2 Короткі теоретичні відомості
Інтеграл — центральне поняття інтегрального числення, узагальнення поняття суми для функції, визначеній на континуумі.
Метод Сімпсона є одним із методів чисельного інтегрування. Названий на честь британського математика Томаса Сімпсона(1710—1761).
Формулою Сімпсона
називається інтеграл від інтерполяційного
многочлена другого степеня на
відрізку 
:
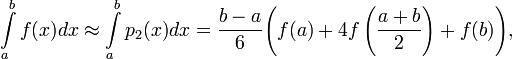
де 
, 
і 
—
значення функції у
відповідних точках .
Найвищої алгсбраічної степені точності квадратурна формула для проміжку [а, b] = [-1, 1] і ваги р (х) = 1 з двома фіксованими вузлами - кінцями проміжку [-1, 1]. Л. к. ф. має вигляд:
Вузли
xj-
корені ортогонального на [-1, 1] з вагою
1 - х 2 многочлена
(многочлена Якобі),
Алгебраїчний ступінь точності дорівнює 2n + l.
Формула встановлена Р. Лобатто
8.3 Програма
%Integrirovanie prostoe
clc
clear all
syms x
y='x/sqrt(x^2+3)'
int(y,'x',1,2.6)
clc
clear all
disp('integrirovanie po Simsonu')
Q=quad(inline('x./(sqrt(x.^2+3))'),1,2.6)
clc
clear all
disp('integrirovanie po Labatto')
Q=quadl(inline('x./(sqrt(x.^2+3))'),1,2.6)
8.4 Результати
y = x/sqrt(x^2+3)
ans = (2*61^(1/2))/5 – 2
integrirovanie po Simsonu
Q = 1.1241
integrirovanie po Labatto
Q = 1.1241