5.3(1) Програма

%f(x)=e^x-sin(x) a=0 b=1

%f(x,y)=e^(y^2-x)+e^x

%Метод перебору

clc

clear all

a=0

b=1

step=0.1

y1=exp(a)-sin(x)

ezplot('exp(x)-sin(x)',[-8,8])

grid on

n=0

hold on

x=a

while x<b

x=x+step

y2=exp(x)-sin(x)

n=n+1

plot(x,y2,'o')

if(y2>y1)

x=x*step

y=exp(x)-sin(x)

n

break

end

y1=y2

end

hold off

5.3(2) Програма

clc

clear all

%Метод дихотомії

a=-0.5

b=0.5

E=0.001

y1=exp(a)+1/a

ezplot('exp(x)+1/x',[-8,8])

n=0

grid on

hold on

while (abs(b-a)>E)

L=b-a

x0=a+L/2

x1=a+L/4

x2=b-L/4

y0=exp(x0)+1/x0

y1=exp(x1)+1/x1

y2=exp(x2)+1/x2

plot(x1,y1,'o')

plot(x2,y2,'x')

n=n+1

if(y1<y0 & y0<y2)

b=x2

else if(y1>y0 & y0>y2)

a=x1

else

a=x1

b=x2

end

end

x0=(x1+x2)/2

n

end

5.4(1) Результат

a =0

b = 1

step = 0.1000

y1 = 0.4354

n = 0

x =0

x = 0.1000

y2 = 1.0053

n = 1

x = 0.0100

y =1.0001

n = 1

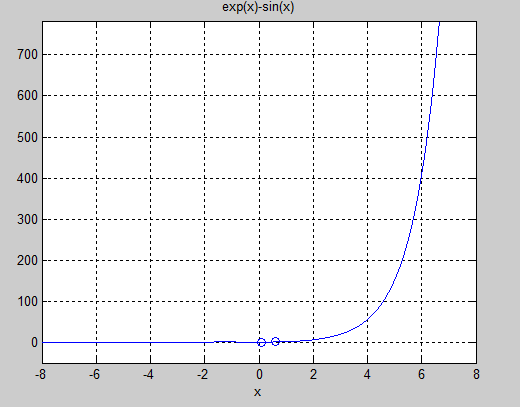
5.4(2) Результат

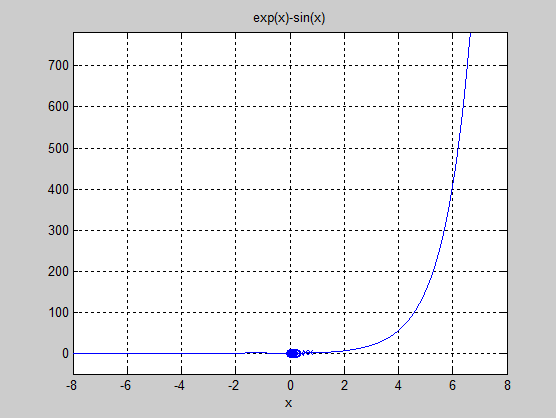
a =-1

b =1

E =0.001

y1 =1.0366

a =0.4882

b =0.4219

x0 =0

n =10

6.1 Знайти кубічну, квадратичну та лінійну апроксимацію заданих точок

6.2 Короткі теоретичні відомості

Для того щоб отримати аналітичні залежності, що описують великі масиви даних, використовують методи апроксимації, які основані на тому, що масив даних замінюють простою функцією (лінійною або квадратичною або кубічною або іншою), яка не обов’язково проходить через всі експериментальні точки, але описує тенденції зміни цих даних та забезпечує мінімум суми квадратів відхилень експериментальних даних від цією функції.

Апроксима́ція (лат. approximare — наближати) — наближене вираження одних математичних об'єктів іншими, простішими, наприклад, кривих ліній — ламаними,ірраціональних чисел — раціональними, неперервних функцій — многочленами.

6.3(1) Програма

clc

clear all

x=[0.115;0.120;0.125;0.130;0.135;0.140]

y=[8.65729;8.29329;7.95829;7.64893;7.36235;7.09613]

plot(x,y,'o')

for i=1:6

z(i,1)=1

z(i,2)=x(i)

end

b=inv(z'*z)*z'*y

for i=1:6

ya(i)=0

for j=1:2

ya(i)=ya(i)+b(j)*z(i,j)

end

end

hold on

plot(x,ya)

grid on

hold off

6.3(2) Програма

clc

clear all

x=[0.115;0.120;0.125;0.130;0.135;0.140]

y=[8.65729;8.29329;7.95829;7.64893;7.36235;7.09613]

plot(x,y,'o')

for i=1:6

z(i,1)=1

z(i,2)=x(i)

z(i,3)=x(i)^2

end

b=inv(z'*z)*z'*y

for i=1:6

ya(i)=0

for j=1:3

ya(i)=ya(i)+b(j)*z(i,j)

end

end

hold on

plot(x,ya)

grid on

hold off

6.3(3) Програма

clc

clear all

x=[0.115;0.120;0.125;0.130;0.135;0.140]

y=[8.65729;8.29329;7.95829;7.64893;7.36235;7.09613]

plot(x,y,'o')

for i=1:6

z(i,1)=1

z(i,2)=x(i)

z(i,3)=x(i)^2

z(i,4)=x(i)^3

end

b=inv(z'*z)*z'*y

for i=1:6

ya(i)=0

for j=1:4

ya(i)=ya(i)+b(j)*z(i,j)

end

end

hold on

plot(x,ya)

grid on

hold off

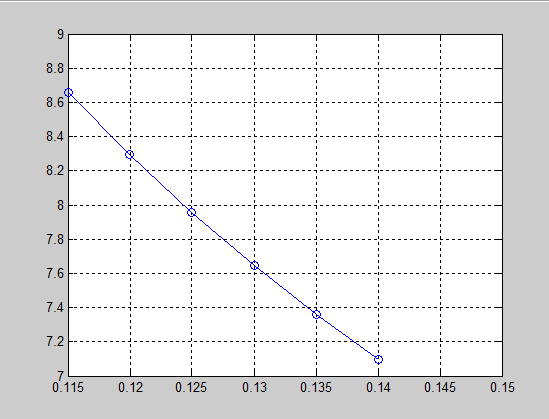
6.4(1) Результати

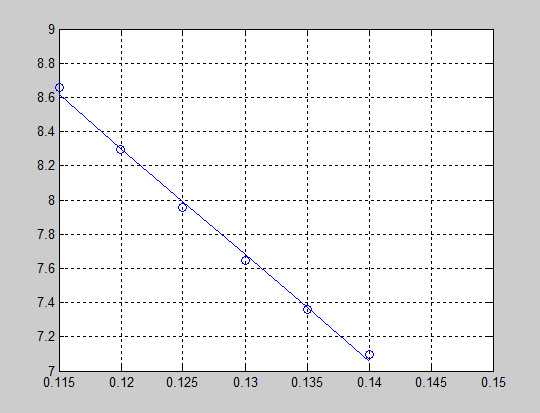
6.4(2) Результати

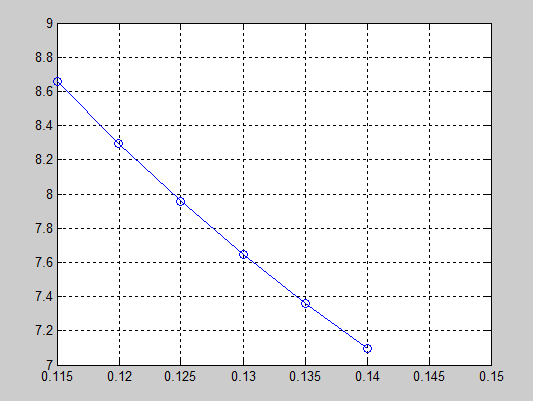
6.4(3) Результати

7.1 Знайти похідну функції в точці, використовуючи Matlab

7.2 Короткі теоретичні відомості

Похідна́ — основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границявідношення приросту функції до приросту її аргументу коли приріст гументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною.

Нехай в деякому околі точки x₀ визначена функція f. Якщо ми візьмемо довільне число x в цьому околі, то приріст аргументу (позначається Δx) в цьому випадку визначається, як x−x₀, а приріст функції (Δy) — як f(x)−f(x₀). Тоді, якщо існує границя  , то вона називається похідною функції f в точці x₀.

Похідною функцією даної функції називається функція, що в будь-якій точці області визначення дорівнює похідній даної функції в цій точці.