МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)
Дисциплина: МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Факультет:___Управление,_____курс I ,_______группы___1бАСУ1-3____
Семестр:_____осенний ( I-й )_______2012-2013 учебного года___________
Лектор:_______проф. М.М. Никитин,_(практ.занятий – 68 час. на группу)_
Примерные практические задания для подготовки к экзамену
Найти предел:
Найти производную функций:
Исследовать на экстремум функцию:
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Исследовать на экстремум функцию: 
.
Найти первообразные функций:
Найти:
Найти: 
Найти:
Найти:
Найти: 
Найти: 
Найти: 
Найти:
Найти:
Найти:
Найти:
Найти: 
Найти: 
Найти:
Найти:
Найти: 
Найти: 
Найти: 
Найти:
Найти: 
Найти: 
Найти:
Найти:
Найти:
Найти: 
Найти: 
Найти:
Найти: 
Найти: 
Найти: 
Исследовать на сходимость несобственные интегралы:
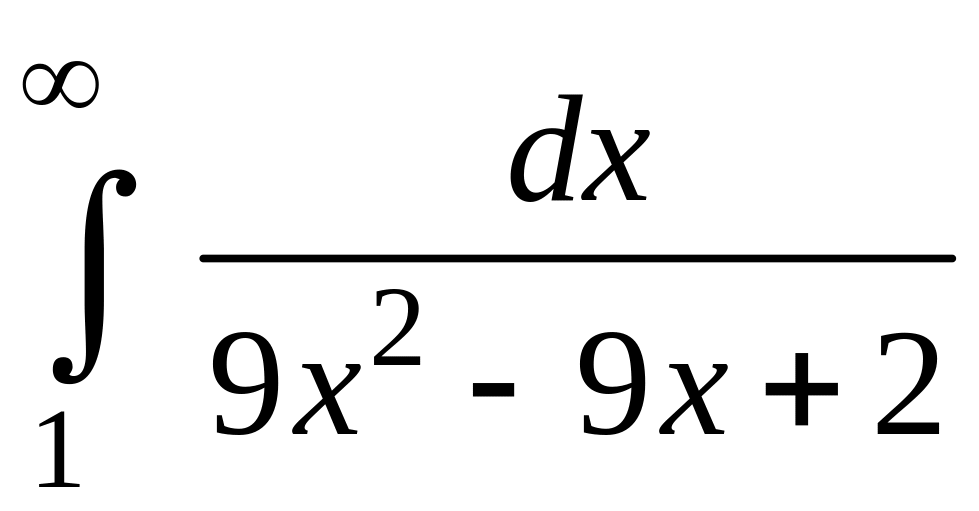
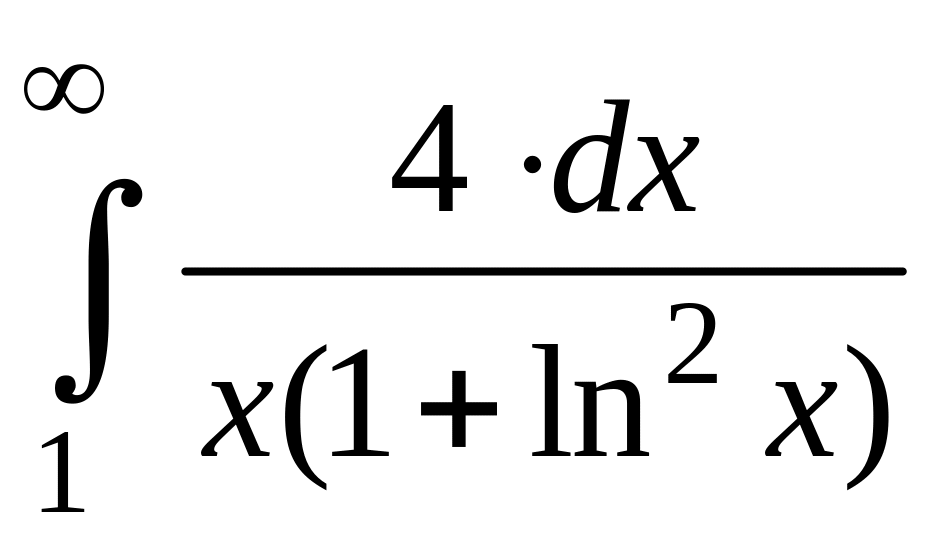
Найти частные производные функции:
Найти частные производные функции:
Найти частные производные функции:
Найти частные производные функции: 
Найти частные производные функции: 
Найти частные производные функции: 
Найти частные производные функции:
Найти частные производные функции: 
Найти частные производные функции: 
Найти частные производные функции: 
В двойном интеграле
перейти к повторному и расставить
пределы интегрирования по области (D),
ограниченной линиями:
.
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
,
.
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
.
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
.
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
В двойном интеграле перейти к повторному и расставить пределы интегрирования по области (D), ограниченной линиями:
Изменить в двойном интеграле
порядок интегрирования:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
.