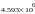Задание 2. Расчет энергетической светимости и проверка закона Стефана-Больцмана.

По формуле Стефана-Больцмана с помощью калькулятора рассчитайте энергетическую светимость черного тела для того же диапазона температур, который указан в задании 1.

Рассчитайте энергетическую светимость с помощью интегралов, подставив пределы 200 нм – ∞ (или большое число, например 10000000 нм ). Сопоставьте полученные значения и результаты занесите в таблицу 3.

Таблица 3

№	Т, К	Энергетическая светимость (калькулятор)	Энергетическая светимость (компьютерный расчет)
1	3000
2	3050	4.907х	4.907х
3	3100
4	3200	5.945х	5.945х
5	3300	6.724х	6.724х

Задание 3 Определение излучательной способности в узком спектральном интервале.

Установить температуру Т_исх (3 колонка табл.1). Из графика для температуры Т_исх определить излучательную способность тела в интервале длин волн, указанных в столбце 4. Приближенно можно считать, что в узком спектральном интервале спектральная плотность энергетической светимости линейно зависит от длины волны. Поэтому излучательная способность в узком спектральном интервале приближенно равна площади трапеции, ограниченной значениями λ₁, λ₂ и r₁, r₂ (см. рисунок 1).

Рассчитайте площадь трапеции с помощью калькулятора.

Рисунок 1

Вычислите излучательную способность в указанном спектральном интервале с помощью определенного интеграла.

Определив излучательную способность в интервале d, найдите частоты ν₁ и ν₂, соответствующие длинам волн λ₁ и λ₂. Результаты запишите в табл. 4.

Откройте файл Plank1.xmcd. Установите требуемую температуру и по графику рассчитайте площадь трапеции в интервале (ν₁ - ν₂)(r_ν1 - r_ν2). Затем рассчитайте излучательную способность в этом интервале частот с помощью интеграла. Занесите результаты вычислений в таблицу 4 и сопоставьте полученные результаты.

Таблица 4

Тисх, К	λ1 ; λ2	ν1 ; ν2	Площадь (λ1 - λ2)( rλ1 – rλ2)	Интеграл	Площадь (ν1 - ν2)(rν1– rν2)	Интеграл
4100	550; 600	550х1012; 600x1012	15	7.185x10-9	15x1012	7.167x10-9

Задание 4. Сопоставление результатов расчетов по формулам Планка и Рэлея–Джинса.

Проанализируйте графики распределения спектральной плотности излучательной способности, рассчитанные по формулам Планка и Рэлея–Джинса . Откройте файл Plank1.xmcd и файл Reley.хmcd и определите спектральную плотность излучательной способности для одной и той же частоты из графиков, построенных по формулам Планка и Рэлея–Джинса для исходной температуры Т_исх (колонка 3). Определите разницу в спектральной плотности излучательной способности Проделайте это и для других частот (6-7 значений), результаты занесите в таблицу 5 и постройте график зависимости от . Проэкстраполируйте пунктирной линией график для больших частот.

Таблица 5

Т_исх =

№	ν, Гц	r(ν) по Планку	r(ν) по Рэлею-Джинсу	Расхождение Δr
1	550	1.047x10e-8	6.205x10e-4	0,00062048953
2	560	9.801x10e-9	6.433x10e-4	0,00064329020
3	570	9.166x10e-9	6.664x10e-4	0,00066639083
4	580	8.563x10e-9	6.9x10e-4	0,00068999144
5	590	7.994x10e-9	7.14x10e-4	0,00071399201
6	600	7.456x10e-9	7.384x10e-4	0,00073839254

Контрольные вопросы

1. Сформулируйте законы теплового излучения черного тела.

2. Как из графиков определить энергетическую светимость черного тела?

3. Почему отличаются максимумы кривых распределения энергии в координатах  и  на графиках?

4. Законы теплового излучения до работ Планка были получены теоретически или установлены экспериментально?

5. Из формулы Планка выведите закон Рэлея-Джинса.

6. Почему расхождение результатов расчета по формулам Планка и Рэлея–Джинса получило в истории физики название «ультрафиолетовая катастрофа»?