
Выводы.
Параболическое уравнение значимо лучше описывает экспериментальные данные зависимости плотности пара от температуры, так как расчетное значение критерия Фишера 42.5 значительно превышает табличное равное 3.97. Следовательно, включение квадратичного члена в полиномиальное уравнение имеет смысл.
Графическое представление результатов расчета наглядно демонстрирует сделанные выводы.
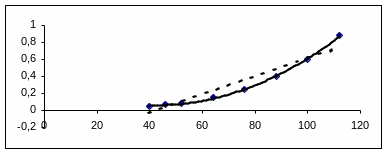
Пунктирная линия- уравнение линейной регрессии; сплошная линия – параболической регрессии, точки на графике – экспериментальные значения.
-
Нахождение параметров зависимости вида y(t)=a0+a1t+a2t2
Плотность водяного пара на линии насыщения r(t)=a0+a1t+a2t 2
№
ti, °C
ri, ом
ti2
tiri
ti3
ti4
ti2ri
r(ti) расч.
∆ri= r(ti) расч.- ri
(∆ri)2
(ri-rср)2
1
40
0,0512
1600
2,05
64000,00
2560000,00
81,84
0,0631
0,01194
0,0001
0,0669
2
46
0,0687
2116
3,16
97336,00
4477456,00
145,33
0,0642
-0,00446
0,0000
0,0582
3
52
0,0811
2704
4,22
140608,00
7311616,00
219,21
0,0773
-0,00377
0,0000
0,0523
4
64
0,1546
4096
9,89
262144,00
16777216,00
633,24
0,1394
-0,01524
0,0002
0,0241
5
76
0,2516
5776
19,12
438976,00
33362176,00
1453,24
0,2493
-0,00235
0,0000
0,0034
6
88
0,3943
7744
34,70
681472,00
59969536,00
3053,46
0,4070
0,01270
0,0002
0,0071
7
100
0,5977
10000
59,77
1000000,00
100000000,00
5977,00
0,6126
0,01489
0,0002
0,0829
8
112
0,8795
12544
98,50
1404928,00
157351936,00
11032,45
0,8660
-0,01348
0,0002
0,3245
сумма
578
2,4786
46580
231,41
4089464,00
381809936,00
22595,77
2,4788
0,0010
0,6194
среднее
0,3098
D1ост2=
0,0085
a0=
3,6129E-01
D2ост2=
0,0002
a1=
-1,4100E-02
Dy2=
0,0885
a2=
1,6613E-04
F=
42.5
r=0,361286-0,0141*t+0,0001661302*t2 FT=3,97 F>FT модель адекватна
