13.5. Запись ротора в виде векторного произведения

Формально rotH можно представить в виде векторного произведения оператора пространственного дифференцирования  на вектор Н, т. е. rotН=[Н]. В этом нетрудно убедиться путем непосредственного умножения  на H:

.

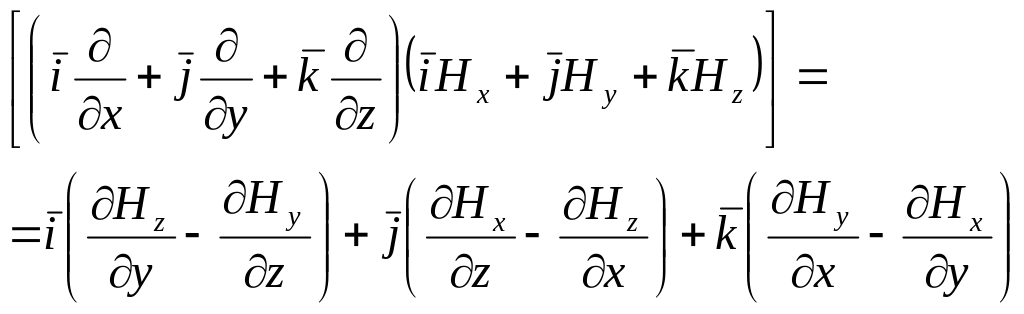13.6. Выражение проекций ротора в цилиндрической и сферической системах координат

Без вывода приведем выражение проекций ротора H:

в цилиндрической системе координат:

;

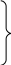; (13.6)

;

в сферической системе координат:

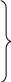
(13.7)

13.7. Принцип непрерывности магнитного потока и запись его в дифференциальной форме.

Магнитный поток есть поток вектора магнитной индукции через некоторую поверхность . Индекс S под знаком интеграла свидетельствует о том, что интеграл взят по поверхности S. Если поверхность замкнута сама на себя (например, поверхность шара), то поток, пронизывающий замкнутую поверхность, .

Опыт показывает, что вошедший внутрь любого объема магнитный поток равен магнитному потоку, вышедшему из того же объема.

Следовательно, алгебраическая сумма вошедшего в объем и вышед­шего из объема потоков равна нулю:

=0. (13.8)

Выражение (13.8) представляет собой математическую запись принципа непрерывности магнитного потока. Разделим обе части (13.8) на объем V, находящийся внутри замкнутой поверхности S, и найдем предел отношения, когда объем V стремится к нулю:

или div B = 0. (13.9)

Соотношение (13.9) можно трактовать как дифференциальную форму принципа непрерывности магнитного потока. Оно пригодно для любой точки магнитного поля. Следовательно, в любой точке этого поля нет ни истока, ни стока линий вектора магнитной индукции. Линии вектора В нигде не прерываются, они представляют собой замкнутые сами на себя линии (окружность- пример замкнутой на себя линии). Но линии Н в точках, где изменяется J (например, на границах сред с разными ), прерывны. Это следует из (13.9):

div B = div ₀ (Н + J} = 0.

Отсюда div H = —div J. Сопоставьте с прерывностью линии Е и непрерывностью линии D в электрическом поле.

13.8. Магнитное поле в областях «занятых» и «не занятых» постоянным током

Вихревыми принято называть поля, ротор которых отличен от нуля. Так как для магнитного поля постоянного тока rot H = , то во всех точках пространства, где   0, поле вектора H является вихревым. В областях пространства, где  = 0, rot Н = 0, магнитное поле можно рассматривать как потенциальное.

13.9. Скалярный потенциал магнитного поля

Для совокупности точек, где  = 0, rot Н == 0, магнитное поле можно рассматривать как потенциальное, т. е. как поле, каждая точка которого имеет скалярный магнитный потенциал _m. Следовательно, для таких областей можно принять

H = - grad _м. (13.10)

Так как div В = div _a Н = 0, то при _a = const div Н = 0.

Подставив в последнее выражение-grad _м, вместо Н, получим

div grad _м = 0.

Таким образом, скалярный потенциал магнитного поля _м, о котором может идти речь только для областей, не занятых током, подчиняется уравнению Лапласа:

²_м=0. (13.11)

Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2

U_м12 = _м1 - _м2 = .

Падение магнитного напряжения между точками 1 и 2 по какому-то одному пути (например, по пути 132, рис. 13.5, а) равно падению магнитного напряжения между теми же точками по какому-то другому

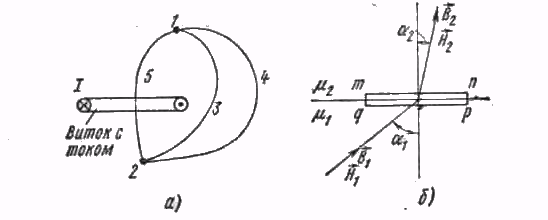
Рис.13.5 Падение магнитного напряжения между точками 1 и 2 может иметь разные значения в зависимости от пути интегрирования.

Пути (например, по пути 142) в том случае, когда эти пути образуют замкнутый контур, ток внутри которого равен нулю. Если же замкнутый контур, образованный двумя путями, охватывает некоторый ток, то падение магнитного напряжения по первому пути не равно падению магнитного напряжения по второму пути — они будут различаться на величину тока, охваченного контуром. Последнее вытекает из закона полного тока.

Так, применительно к рис. 13.5,а (ибо из закона полного тока следует, что ,или ). Следовательно, для того чтобы разность магнитных потенциалов между двумя точками магнитного поля не зависела от пути, надо наложить запрет на прохождение через контур (виток) с током, мысленно натянув на этот контур некоторую пленку. При прохождении через эту пленку _м изменяется скачком на величину тока в контуре.

Следует различать понятия «падение магнитного напряжения» и «магнитное напряжение». Первое определяется только линейным интегралом от Н на dl по выбранному пути. Второе — не только этим интегралом, но и м.д.с., имеющейся на пути. Здесь имеется полная аналогия с понятиями «падение напряжения» и «напряжение» в электрической цепи.