4.Свойства функций непрерывных на отрезке.
Определение. Функция называется непрерывной на отрезке, если она непрерывна в каждой точке этого отрезка.
Рассмотрим некоторые свойства непрерывных функций на отрезке, которые сформулируем в виде теорем.
Теорема1.
(об ограниченности непрерывной функции
на отрезке, первая теорема Вейерштрасса
(немецкий математик 1815-1897 г.)). Если
функция
определена
и непрерывна на отрезке
,
то она ограничена на этом отрезке.
Замечание.
Теорема неверна, если отрезок
заменить интервалом
.
Так, например, функция
непрерывна на
,
но не ограничена, т.к.
.
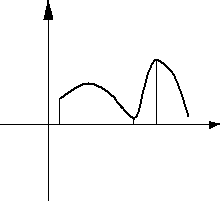
Теорема2. (вторая теорема Вейерштрасса о существовании наибольшего и наименьшего значения).
Если функция непрерывна на отрезке , то она принимает на этом отрезке наибольшее и наименьшее значение.
y
y=f(x)
M
m
0 a x1 x2 x
Теорема утверждает,
что существует хотя бы одна такая точка
и
,
что
и
.
Теорема3. (первая теорема Больцано – Коши (Больцано – чешский математик 1781-1848) о существовании промежуточных значений).
П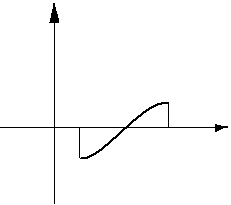
усть
функция
непрерывна
на отрезке
и на концах отрезка имеет значения
разных знаков. Тогда существует точка
,
в которой
.
y
f(в)
0 a c в x
f(a)
Геометрический смысл теоремы: непрерывная кривая при переходе из одной полуплоскости, границей которой является ось абсцисс, в другую пересекает эту ось.
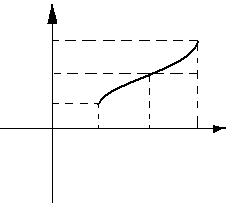
Теорема4.(вторая теорема Больцано – Коши)
Пусть функция
непрерывна
на отрезке
,
причем
.
Пусть C
– любое число, заключенное между A
и B.
Тогда на отрезке
найдется такая точка C,
что
.
у
у=f(x)
В
С
А
0 f(a) f(c) f(в)
a c в х
С геометрической
точки зрения, всякая прямая
пересекает график функций
.
Заключение.
При введении понятия непрерывной функции мы отмечали, что определение непрерывности должно хорошо согласовываться с тем интуитивным представлением о непрерывности какого-либо процесса или непрерывности линии, которое нами получено из практики, из повседневного опыта. Однако из того математического определения непрерывной функции, которое было дано в лекции, не видно, обладают ли функции, непрерывные в указанном смысле, теми свойствами которые естественны для всякого непрерывного процесса. Другими словами, мы должны оправдать данное математическое определение непрерывности функции, показать его пригодность для изучения непрерывных процессов.