20. Графы
граф — это совокупность непустогомножества вершин и множества пар вершин (связей между вершинами).
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Граф,
или неориентированный
граф 
—
это упорядоченная
пара 
,
для которой выполнены следующие условия:
—
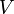это
непустое множество вершин или узлов,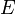
—
это
множество пар (в случае неориентированного
графа — неупорядоченных) вершин,
называемых рёбрами.
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Циклом называют
путь, в котором первая и последняя
вершины совпадают. При этом длиной пути
(или цикла) называют число составляющих
его рёбер.
Заметим, что если вершины 
и 
являются
концами некоторого ребра, то согласно
данному определению, последовательность 
является
циклом. Чтобы избежать таких «вырожденных»
случаев, вводят следующие понятия.
21. Теорема о реализуемости графов в трехмерном евклидовом пространстве ?
22. Теорема Понтрягина-Куратовского
Очевидно утверждение: если граф G содержит подграф, гомеоморфный K5 или K3,3, его невозможно разложить на плоскости. Оказывается, верно и обратное.
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфныхполному графу из пяти вершин (K5) или графу «домики и колодцы» (K3,3). |
Теорему также можно сформулировать в следующем варианте (иногда его называют «теорема Вагнера»).
Граф планарен тогда и только тогда, когда не содержит подграфов, стягивающихся в K5или K3,3. |
[Править]Признаки непланарных графов
достаточное условие — если граф содержит двудольный подграф K3,3 или полный подграф K5, то он является не планарным;
необходимое условие — если граф не планарный, то он должен содержать больше 4 вершин, степень которых больше 3, или больше 5 вершин степени больше 2.
23.Основные типы графов
Основные типы графов
Граф называется пустым, если E(G) = , т.е., если в нем нет ребер. Пустой граф порядка n обозначается 0n. Граф 01 называется тривиальным. Граф, в котором любые две вершины соединены ребром называется полным. Полный граф порядка n обозначается Kn.
|
|
|
|
Нетрудно подсчитать, что граф Kn им еет n(n-1)/2 ребер.
Граф такого вида, как на рис. 1, называется простой цепью. Простая цепь порядка n обозначается Pn (на рисунке 1 изображена цепь P4). Простая цепь Pn имеет n –1 ребер.
Замкнутые цепи, т.е. такие графы, как на рис. 2, называются простыми циклами. Простой цикл порядка n обозначается Cn (на рис. 2 изображена простая цепь С7). Понятно, что простая цепь Cn имеет столько же ребер, сколько и вершин, т.е. n.
Г
рафы,
такие как на рис. 3, называются колесами.
Колесо порядка n+1 обозначается Wn (на
рис. 3 изображено колесо W7); оно имеет
2n ребер.
Г
раф
называется двудольным, если множество
его вершин можно разбить на два непустых
подмножества (доли) так, что никакие две
вершины одной доли не являются смежными.
(Аналогично определяются трехдольные,
четырехдольные и т.д. графы.) Таким
образом, в двудольном графе смежными
могут быть только вершины из разных
долей (не обязательно каждая с каждой).
Пример двудольного графа см. на рис. 4.
Если же в двудольном графе любые две вершины из разных долей соединены ребром, то такой граф называется полным двудольным. Полный двудольный граф с n вершинами в одной доле и с m вершинами -- в другой обозначается Kn,m. См. примеры:
Г
рафы
K1,n называется звездными графами, или
звездами.
Легко видеть, что граф Kn,m является (n+m, nm)-графом, т.е. имеет n+m вершин и nm ребер.
Понятно, что существуют графы, которые можно одновременно отнести к нескольким типам. Например, K3 = C3, K2 = P2, K2, 2 = C4, K4 = W3.
Соотношение, характеризующее зависимость между координатами х и у точек кривой называется уравнением этой кривой. Например: у+2х-1=0 - уравнение прямой, х2+у2=4 - уравнение окружности. Координаты любой точки, лежащей на кривой, удовлетворяют уравнению кривой, а координаты точек, на кривой не лежащей, уравнению не удовлетворяют. Например, проверим лежит ли точка А (1,2) и В (0,1) на прямой у+2х-1=0. Для этого подставим координаты каждой точки в уравнение прямой. 1) А(1,2)-2+2-1 0, вывод: точка А не принадлежит прямой. 2) В(0,1)-1-1=0, вывод: точка В лежит на прямой.