11. Минимизация переключательных функций. Метод диаграм Вейча.

Минимизацию логических функций можно провести, используя диаграммы Вейча (или аналогичный метод карт Карно). Диаграмма Вейча для функции F четырех переменных А, В, С, D представлена на рис. 4.13. Каждая из переменных принимает два значения, т. е. возможны   комбинаций входных функций. Диаграмма Вейча содержит 16 клеток, каждая из которых соответствует одной из 16 возможных комбинаций входных переменных. На полях диаграммы обозначены значения каждой переменной. Диаграмма состоит   четырех строк и четырех столбцов.

Рассмотрим минимизацию логической функции на примере.

Дано: Упростить функцию  .

Решение разбиваем на четыре операции.

1. Преобразование исходного выражения. При преобразовании необходимо раскрыть скобки и исключить знаки инверсии над комбинацией переменных. Последнее осуществляется с помощью формул де Моргана. Получим

2. Заполнение диаграммы Вейча проводим при наличии в полученном выражении соответствующих комбинаций входных переменных, эти клетки обозначаются знаком 1 (рис. 4.14,а). Если слагаемое не содержит одного или нескольких переменных, то должны заполняться клетки, соответствующие и прямому, и инверсному значениям отсутствующей переменной.

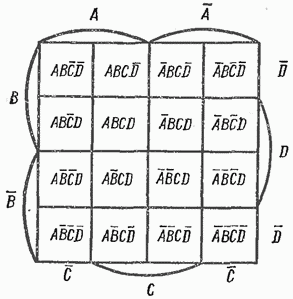
Рис. 4.13. Диаграмма Вейча для функции четырех переменных

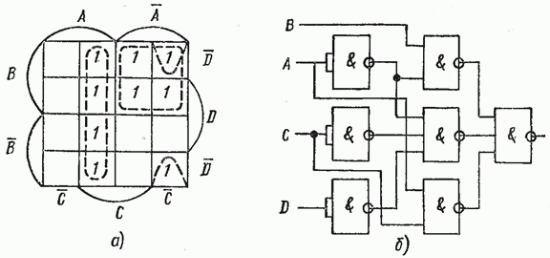
Рис. 4.14. К минимизации схемы логического комбинационного устройства: а — диаграмма Вейча; б — схема на элементах 

Например:  . Заполняются клетки ABCD и ABCD.

3. Производится «склейка» клеток. Можно склеить (т. е. объединить, лак показано на рис. 4.14, я) целую заполненную строку, целый столбец, полстроки или полстолбца. Можно склеить соседние строки, столбцы, полустроки и полустолбцы. Склейки можно располагать через границы диаграммы Вейча, т. е. объединяя нижиий и верхний, правый и левый края. Одиа склейка может накладываться на другую. Склейки содержат 2, 4, 8 клеток.

Для успешной минимизации нужно расположить на таблице минимальное количество склеек, каждая из которых содержит наибольшее количество клеток.

Склейки для логической функции F показаны на рис. 4.14, а.

4. Расшифровка склеек. Каждая склейка представлена в виде конъюнкции переменных. Второй столбец на диаграмме рис. 4.14, я расшифровывается как АС, так как он охватывает и прямые, и инверсные значения переменных В и D, т. е. от В до D не зависит. Склейка в правой верхней части таблицы расшифровывается как АВ, а склейка из двух клеток в четвертом столбце соответствует ACD. Результат минимизации:

На рис.   приведена схема на элементах  , реализующая функцию F. При построении схемы использованы стандартные решения, приведенные на рис. 4.11.

Процедура минимизации функций с помощью диаграмм Вейча очень проста, и ее использование заменяет путь сложных преобразований с помощью тождеств. С помощью диаграмм Вейча можно минимизировать и функции трех переменных, при этом  , т. е. из диаграммы исключают первую и четвертую строки, диаграмма содержит только восемь клеток.

12. Совершенная дизъюктивная и совершенная конъюктивная нормальная формы

Следствие 1 (Совершенная дизъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме:^*

f(x1,...,xm) =   x1s1 & ... & xmsm & f(s1,...,sm) =   *

=   x1s1 & ... & xmsm

Следствие 2 (Совершенная конъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме:^*

f(x1,...,x_m) =   x1^¬s₁ Ъ ... Ъ x_m^¬s_m

Таким образом, любая булева функция может быть представлена суперпозицией конъюнкции, дизъюнкции и отрицания. Разложение по всем переменным в дизъюнкцию называется совершенной дизъюнктивной нормальной формой функции, а в конъюнкцию – совершенной конъюнктивной нормальной формой.^*

Совершенная дизъюнктивная и конъюнктивная нормальная формы дают способ представления булевой функции через суперпозицию конъюнкции, дизъюнкции и отрицания если у нас есть таблица значений функции.

Чтобы получить совершенную дизъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.

Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.