42. Теорема о числе различных цепей длины n в графах и орграфах
43. Теорема о максимальном числе ребер в графе с р вершинами и q компонентами связности
Теорема Ту́рана даёт ответ на вопрос о максимальном количестве рёбер в графе без полного n-вершинного подграфа.
Обозначим
через 
полный
n-вершинный граф.
Определим
граф 
с
вершинами
следующим образом. Разобьём все вершины
на
«почти
равных» групп (то есть возьмём 
групп
по 
вершине
и 
групп
по 
вершин,
если 
с
остатком
)
и соединим рёбрами все пары вершин из
разных групп. Т.о. получим
-дольный
граф.
Будем
обозначать через 
максимальнео
количество рёбер, которое может иметь
граф с
вершинами,
не содержащий подграфа, изоморфного
.
-
Среди всех графов на вершинах, не содержащих подграфа , максимальное количество рёбер имеет граф . Если
,
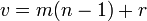где
—
остаток от деления
на
,
то этот максимум равен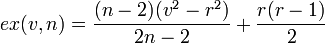
При 
основную
формулу можно записать короче: 
.
Доказательство можно провести, например, с помощью математической индукции по количеству вершин графа
44. Разрез транспортной сети и его свойства
Разрез (s-t
cut) — разбиение множества всех вершин
V на два подмножества, A и B, таких что 
, 
.
Минимальный разрез - разрез с минимальной пропускной способностью