8.2. Фазовые кривые мтз.

Фазовые кривые в методе МТЗ строят обычно для импеданса, представляющего собой отношение сопряженных компонент или . Фаза импеданса, соответственно, определяется на логарифмической шкале как разность фаз сопряженных компонент.

(8.9)

где , - значения фазы отдельных компонент в градусах.

Входной импеданс над однородным полупространством имеет вид . Учитывая что , фаза импеданса над однородным полупространством имеет значение

(8.10)

То есть график фазы импеданса над однородной средой имеет вид горизонтальной прямой на уровне -45º и не зависит от сопротивления среды и периода колебаний.

Над слоистым разрезом, в соответствии с (8.1) фаза импеданса определяется выражением

(8.11)

Поскольку изменяется от +45⁰ до -45⁰ (раздел 8.1), то фаза импеданса над слоистым полупространством изменяется от 0 до -90⁰

Подобно амплитудным, фазовые кривые отражают изменение удельного сопротивления и мощности слоев с глубиной, но только качественно, с точностью до некоторой неизвестной постоянной. Никакой новой информации об устройстве среды кривые фазы импеданса не приносят. Они могут быть получены из амплитудных кривых импеданса путем их дифференцирования, пользуясь дисперсионными соотношениями П. Вайдельта.

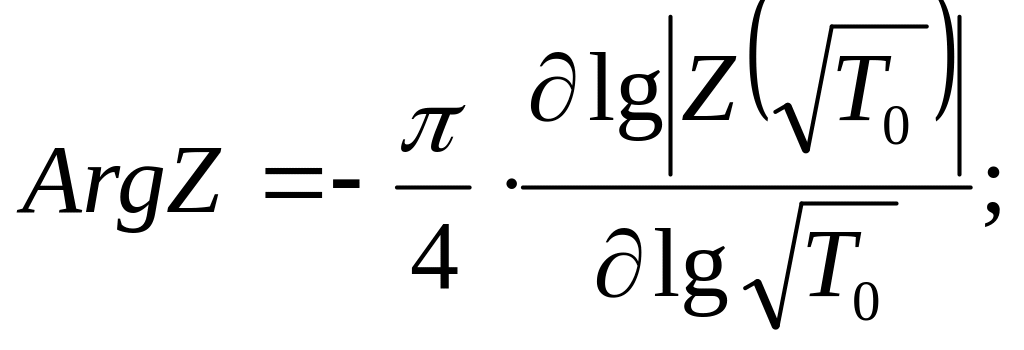(8.12)

Фазовые кривые строят в линейно-логарифмическом масштабе: по оси ординат откладываются значения в градусах в линейном масштабе, по оси абсцисс, в логарифмическом масштабе – значения , где Т- период в секундах. Из рассмотрения (рис. 8.1) можно видеть, что породы высокого сопротивления приводят к уменьшению абсолютных значений разности фаз между компонентами импеданса, а породы низкого сопротивления – к обратной картине. На рис. 8.1 можно видеть, что при (разрез 1 в таблице) кривая фазы импеданса завершается горизонтальным участком (кривая 1). Наоборот, при (разрез 2 в таблице) кривая фазы импеданса завершается горизонтальным участком (кривая 2). Если же основание разреза имеет конечное сопротивление (разрез 3 на рис 8.1), то фаза импеданса, испытав минимум или максимум, возвращается к уровню -45˚, отмеченному выше для однородного полупространства.

При интерпретации МТЗ фазовые кривые импеданса играют роль дополнительной информации, улучшающей качество и достоверность результатов решения обратной задачи. В процессе итерационного решения обратной задачи идет непрерывный поиск согласия между фазовыми и амплитудными кривыми.

Иногда, принято строить фазы кажущегося сопротивления. В этом случае соотношения Питера Вайдельта приобретают вид

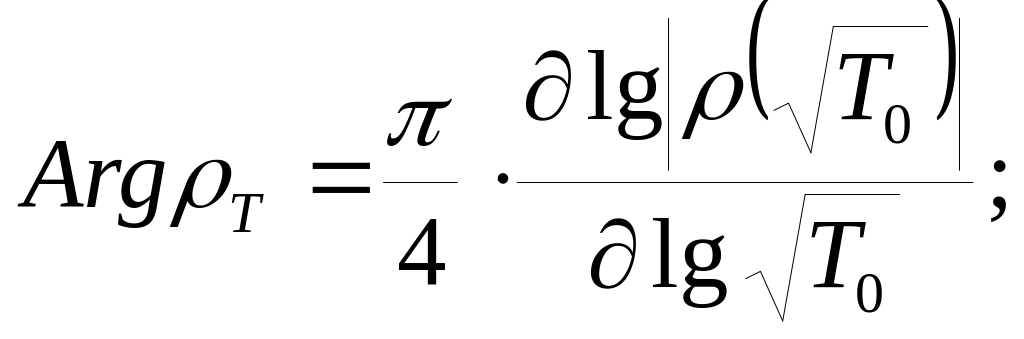(8.13)

По внешнему виду формулы (8.12) и (8.13) отличаются только знаками. Но это не означает, что графики фазы импеданса и фазы сопротивления одинаковы по форме. Вид их существенно различен, так как разный вид имеют графики и .

Поскольку мы уже знаем из раздела 8.1, что производная в выражении (8.13) изменяется от 2 для разреза ( ) до -2 для разреза ( ), то соответствующие значения фазы кажущегося сопротивления над слоистым полупространством изменяются в пределах от +90⁰ для восходящей кривой над разрезом с изолирующим основанием до -90⁰ для нисходящей кривой над разрезом с бесконечно проводящим основанием. Общая картина поведения фазы кажущегося сопротивления сохраняет вид такой же, который был описан для фазы импеданса.