7. Горизонтально-слоистая модель

Определение поля плоской электромагнитной волны на поверхности горизонтально-слоистого полупространства является фундаментальной задачей магнитотеллурики. Такая модель называется одномерной. Ее описание приведено на рисунке 7.1. Модель состоит из N горизонтально однородных изотропных слоев, каждый из которых характеризуется определенными и постоянными значениями удельного сопротивления

и мощности . Значения относительной диэлектрической и магнитной проницаемости слоев приняты равными единице. Мощность нижнего, N-го слоя равна бесконечности. Земная поверхность совпадает с плоскостью ХУ декартовой системы координат x,y,z. Ось z направлена сверху вниз. Верхнее полупространство (z<0) заполнено непроводящим воздухом.

П усть по оси z сверху вниз распространяются две первичные, плоские монохроматические электромагнитные волны и , эллиптически поляризованные в плоскости ХУ.

Процедура скаляризации позволяет представить полные вектора и в виде суперпозиции скалярных составляющих по ортам.

(7.1)

их скалярное произведение имеет вид:

Вспомним, что из условия осевой симметрии среды и из определения импеданса плоской волны следует:

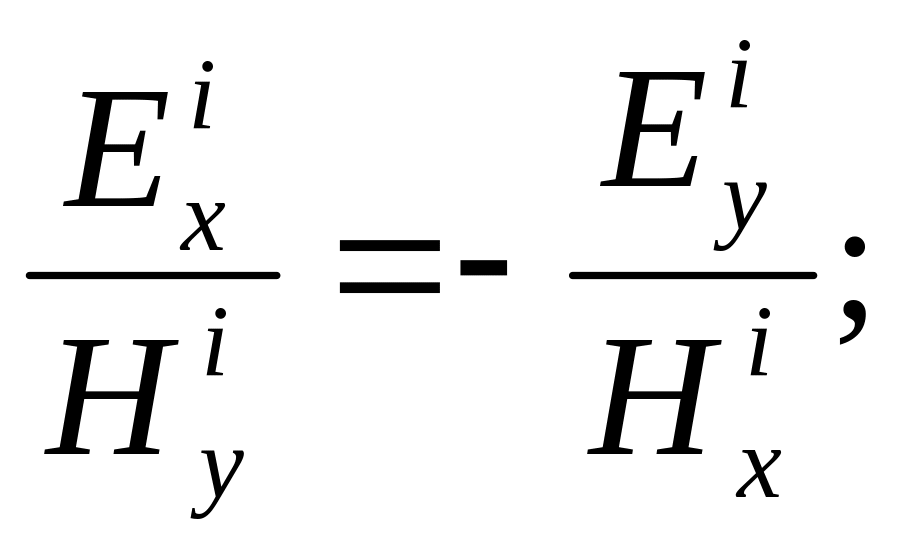
Следовательно, скалярное произведение . Отсюда следует вывод, что комплексные вектора и всегда ортогональны между собой. Из ортогональности векторов и , а так же из (6.29) следует, что для определения импеданса на поверхности горизонтально-слоистой модели достаточно определить значение одной из сопряженных пар, например, составляющих Е_х и Н_у электромагнитного поля. Учитывая четвертый постулат модели Тихонова-Каньяра (уравнение 5.4), чтобы определить скалярную составляющую , достаточно решить одномерное уравнение Гельмгольца в декартовой системе координат.

, (7.2)

где - волновое число n-го слоя.

Общее решение уравнения (7.2) имеет вид

, (7.3)

где и (n=1,2,…N) – некоторые, постоянные для каждого n-го слоя составляющие напряженности электрического поля по орту , зависящие от двух параметров – от удельного сопротивления n-го слоя и от частоты. Убывающая с ростом глубины z экспонента определяет совокупность плоско-однородных волн, распространяющихся сверху вниз, а возрастающая с ростом z экспонента - совокупность отраженных волн, распространяющихся снизу вверх (см. уравнения 6.8 и 6.9).

Для определения сопряженной компоненты магнитного поля Н_у решим второе уравнение Максвелла . Для скалярной компоненты Н_у получим выражение

.

С учетом того, что в плоском поле отсутствуют вертикальные компоненты E_z и H_z и тождественно равны нулю все горизонтальные производные, следует

(7.4)

Подставляя (7.3) в (7.4), найдем

. (7.5)

Таким образом, видно, что магнитное поле может быть выражено через те же константы и , что и электрическое поле .

Теперь найдем, каким образом связан с параметрами среды магнитотеллурический входной импеданс . Найдем из 7.3 и 7.5

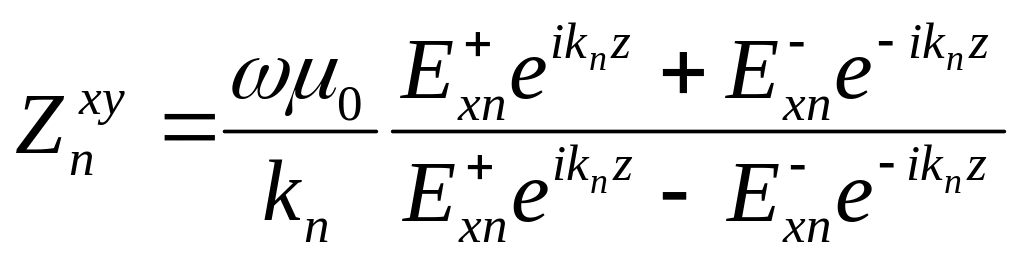(7.6)

Поделим числитель и знаменатель (7.6) на

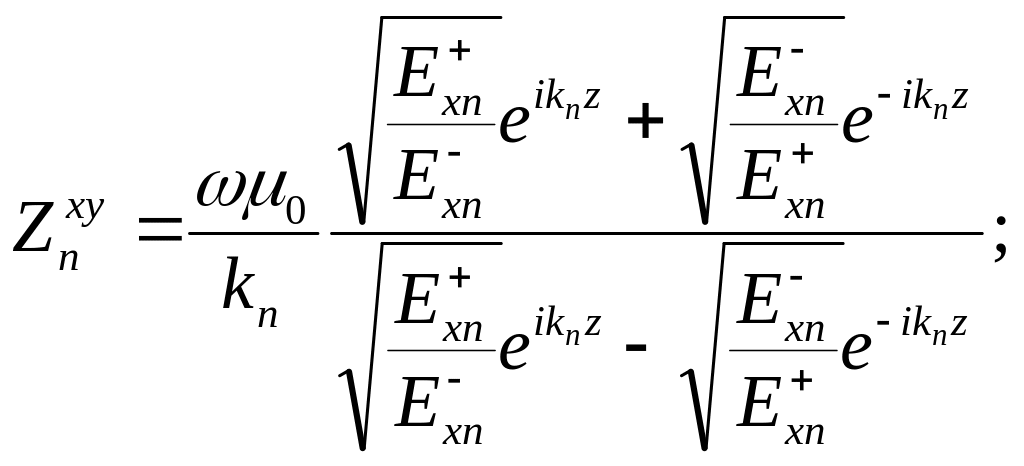(7.7)

Введем обозначение

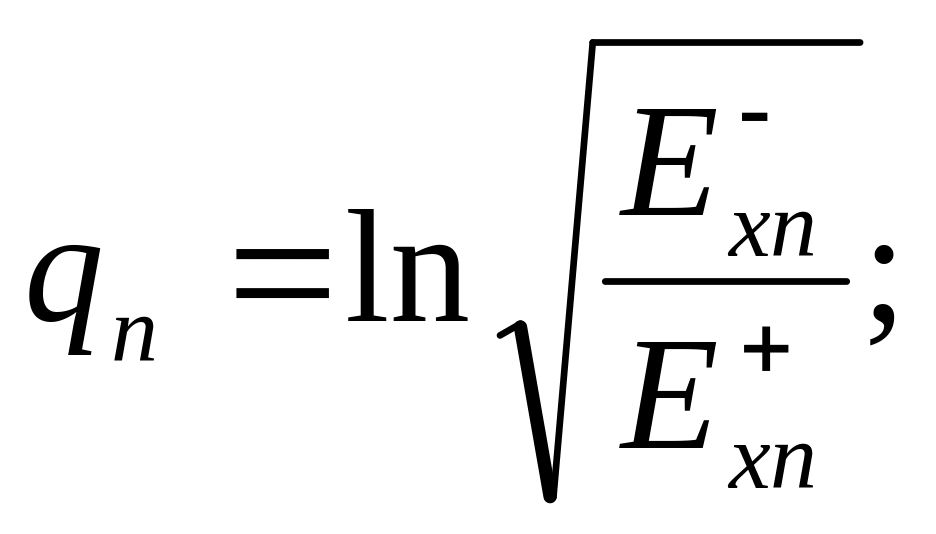
Тогда, 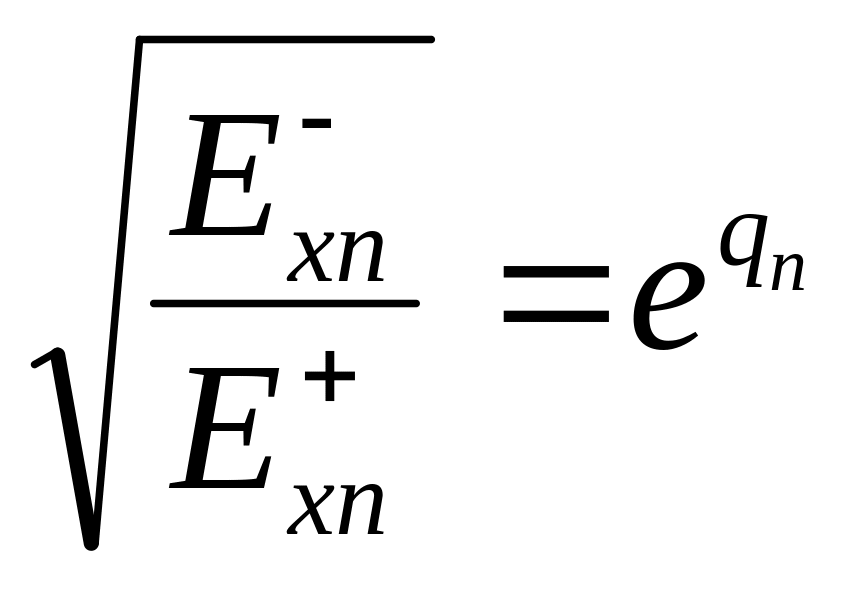и 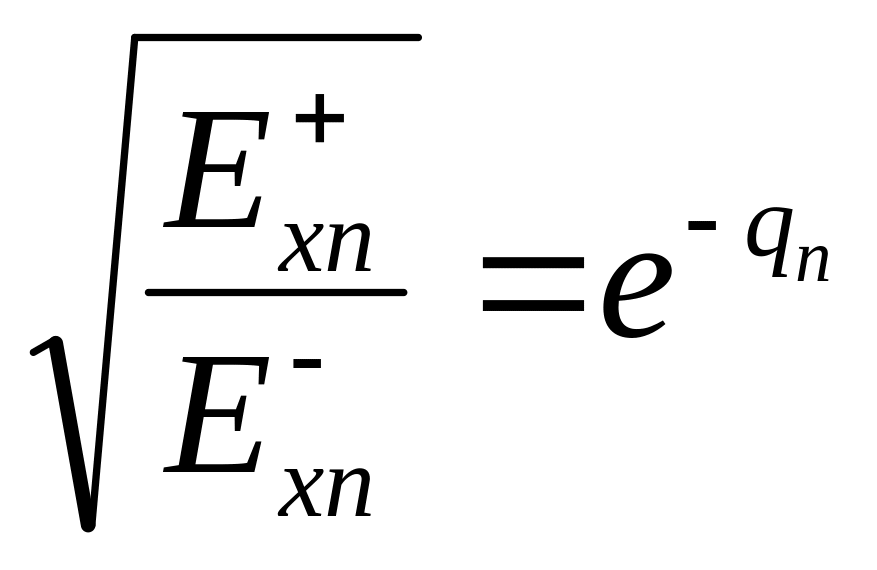, отсюда

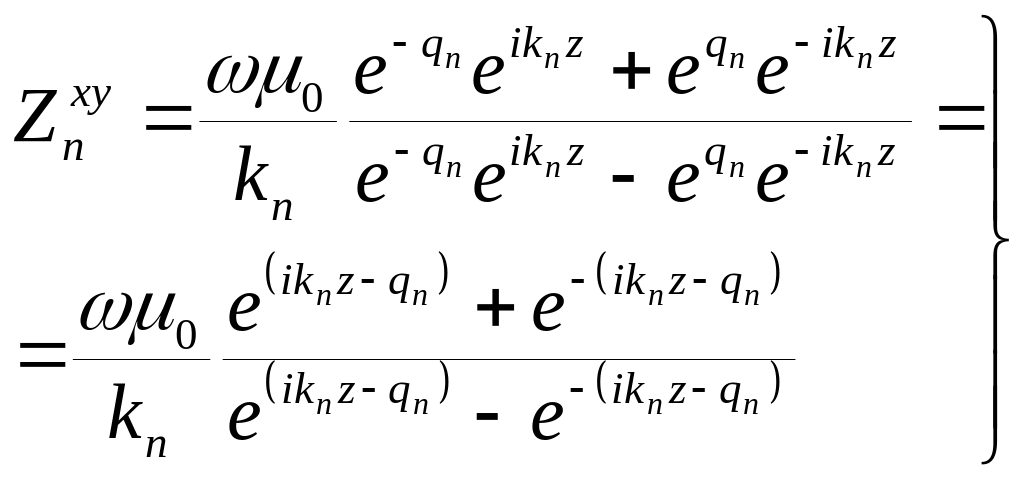
Обозначим , тогда выражение для можно переписать в виде

Далее, пользуясь понятием гиперболического котангенса, приведенным ниже в ссылке, найдем

(7.8)

Из рисунка 7.1 можно видеть, что полученное выражение для импеданса в n-м слое относится к интервалу глубин

z_n-1+0<z<z_n-0

Две неизвестные постоянные и , входящие в (7.8) через выражение , могут быть определены, исходя из граничных условий о непрерывности горизонтальных составляющих поля и на границах слоев. Из них следует заключение о непрерывности их отношения, т.е. импеданса на границах слоев

(7.9)

* Напомним гиперболические функции

(7.9)

В левую часть (7.9) подставим значение из 7.8

Теперь мы можем найти выражение для на верхней стороне i-й границы , используя пока неизвестные значения импеданса на нижней стороне n-й границы

(7.10)

Поскольку ,

то можно переписать (7.10) в следующем виде

(7.11)

Теперь, пользуясь выражением для импеданса , действующего в слое n между его верхней границей и нижней границей , можно найти выражение для рекуррентных соотношений, связывающих магнитотеллурические импедансы двух соседних слоев путем подстановки значений импеданса с кровли нижнего слоя на подошву верхнего слоя . Для этого в выражение (7.8) для импеданса в слое n подставим значение , выраженное в (7.11) через импеданс на кровле слоя n+1.

(7.11а)

Если теперь подставить (7.11а) в (7.8), то мы получим выражение

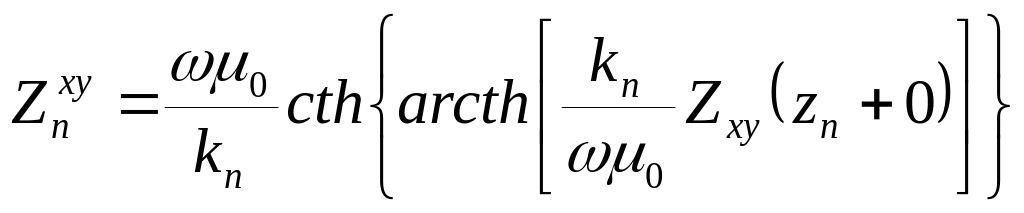(7.11б)

Однако, с учетом граничных условий при переходе с нижнего слоя на верхний, более правильной является следующая формула

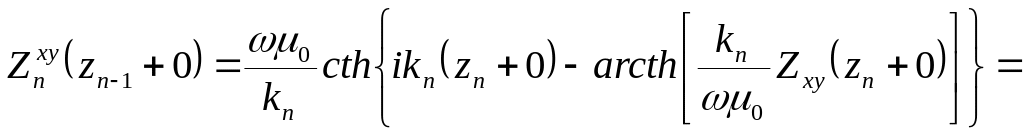
(7.12)

Полученное выражение (7.12) позволяет нам вычислить импеданс в каждом отдельно взятом n-м слое, пользуясь пока еще неизвестным значением импеданса в соседнем, залегающем ниже (n+1)-м слое. Перепишем их по слоям.

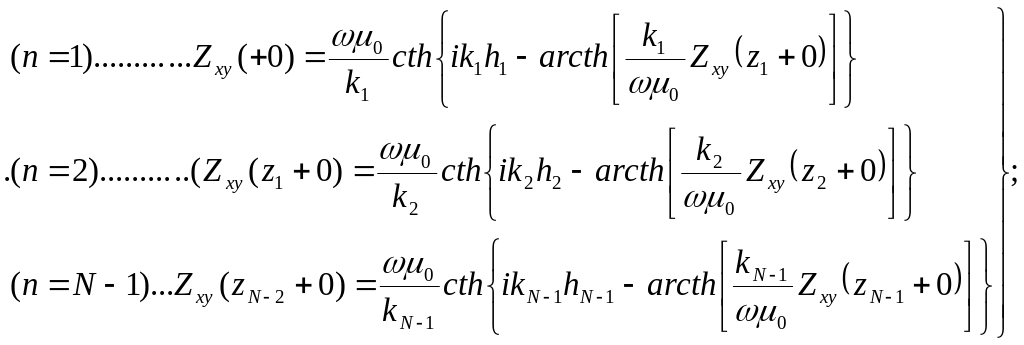(7.13)

Теперь остается определить импеданс в подстилающем N-ом слое бесконечной мощности. Из самых общих соображений нетрудно оценить, что в нем нет отражений, и сохраняются лишь затухающие с ростом z экспоненты в решении уравнения Гельмгольца (7.3)

при (7.14)

Раньше мы записали выражение (7.4) для сопряженной магнитной компоненты . Подставим в него из (7.14)

(7.15)

Можно видеть, что импеданс в основании слоистого разреза определяется явным образом

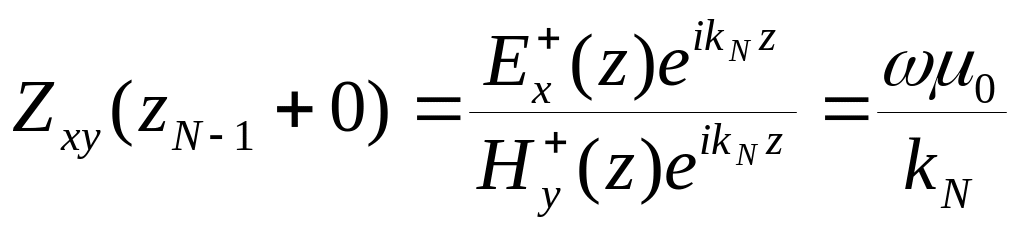(7.16)

В него входят известные, заранее заданные в прямой задаче параметры и . Подставив (7.16) в (7.13), мы полностью определяем импеданс в вышележащем слое (N+1). Продолжая эту операцию в направлении снизу вверх (она называется рекурсией), мы доберемся до верхнего слоя и определим импеданс на поверхности n-слойного полупространства.

(7.16)

Где R_n- приведенный импеданс слоистого полупространства

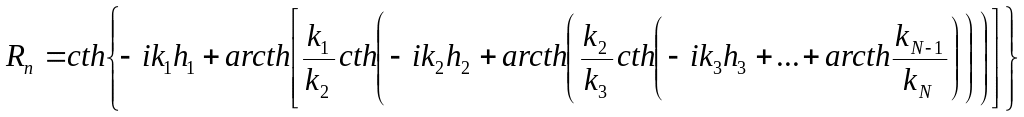7.17)

Для импеданса можно выполнить аналогичные вычисления, и они приведут к тому же результату [2.39, 2.40]. Таким образом, на поверхности слоистого полупространства можно заметить

Его принято называть импедансом Тихонова-Каньяра, понимая под этим входной импеданс горизонтально-слоистого однородного разреза. Вычисляется он по отношению взаимно-ортогональных компонент электрического и магнитного полей, измеряемых на дневной поверхности Земли.

Величина приведенного импеданса может быть определена как результат нормировки (деления) входного импеданса (аномального) на значение импеданса верхнего слоя , принимаемого как «нормальный» импеданс однородного полупространства с удельным сопротивлением .

(7.18)

Отсюда можно записать, что рассчитываемое теоретически значение входного импеданса магнитотеллурического поля над горизонтально слоистой средой равно произведению импеданса Z₁ для однородного полупространства, сопротивление которого равно сопротивлению первого слоя, на приведенный импеданс , отражающий влияние всех залегающих ниже слоев

(7.18а)

Кажущееся сопротивление по результатам описанного выше теоретического решения прямой задачи вычисляют по формуле

(7.18б)