
- •5 Линии передачи. Типы регулярных линий передачи
- •6 Затухание волн в регулярных линиях передачи
- •7 Критическая длина волны в прямоугольном металлическом волноводе.Области прозрачности и отсечки волновода
- •11 Токи на стенках прямоугольного волновода Излучающие и неизлучающие щели.
- •14Критичуская длина волны е и н типа в круглом металлическом волноводе
- •23Основной тип колебаний в прямоугольном и круглом обьемпых резонаторах
- •24Добротность объемных резонаторов
- •29 Мощность элнментарного электрического излучателя.Сопротивление излучения
1uravnenie maksvela dl9 monohramoti4eskogo pol9
Электромагнитные
поля естественного и искусственного
происхождения часто меняются во времени
по гармоническому закону. В линейных
средах, для которых справедлив принцип
суперпозиции, любой реальный
электромагнитный процесс, происходящий
во времени по негармоническому закону,
можно представить как сумму гармонических
составляющих, воспользовавшись
разложением в ряд или интеграл Фурье.
Поэтому изучение электромагнитных
полей, изменяющихся по гармоническому
закону с некоторой постоянной частотой,
имеет большое практическое значение.
Такие поля часто называют также
монохроматическими.
уравнения
Максвелла для монохроматического поля
в комплексной форме:1.
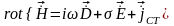 2.
2.
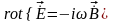 .3.
.3.
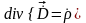 .4.
.4.
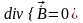 .
5.
.
5.
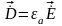 .
.
6.
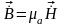 .
.
2Комплексная диэлектрическая проницаемость. Угол диэлектрических потерь
Р ассмотрим
гармонический электромагнитный процесс
в некоторой материальной среде с
конечным значением удельной
проводимости
ассмотрим
гармонический электромагнитный процесс
в некоторой материальной среде с
конечным значением удельной
проводимости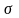 .Объединив
уравнения .
и
из
системы получим:
.Объединив
уравнения .
и
из
системы получим: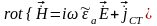 ,где
величин
,где
величин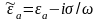 представляет
собой
комплексную диэлектрическую проницаемость
данного
вещества.Введя этот параметр, можно
одновременно учесть как поляризационные,
так и проводящие свойства вещества.
Значение действительной части комплексной
диэлектрической проницаемости описывает
интенсивность процесса поляризации,
в то время как мнимая часть учитывает
плотность токов проводимости Изображая
число
представляет
собой
комплексную диэлектрическую проницаемость
данного
вещества.Введя этот параметр, можно
одновременно учесть как поляризационные,
так и проводящие свойства вещества.
Значение действительной части комплексной
диэлектрической проницаемости описывает
интенсивность процесса поляризации,
в то время как мнимая часть учитывает
плотность токов проводимости Изображая
число
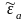 в виде вектора на комплексной плоскости
можно описывать соотношение между
действительной и мнимой частями
комплексной проницаемости при помощи
угла
в виде вектора на комплексной плоскости
можно описывать соотношение между
действительной и мнимой частями
комплексной проницаемости при помощи
угла
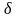 ,
который называют углом
диэлектрических потерь.Чем
больше этот угол, тем значительнее доля
электромагнитной энергии, рассеиваемой
в в виде теплоты при протекании токов
проводимости.В справочных таблицах
обычно приводят значения тангенса
этого угла. В случае анизотропной по
отношению к электрическому полю среды
комплексная диэлектрическая проницаемость
вещества является тензором.Тангес угла
потерь хороших диэлектриков на частотах
электромагнитных колебаний СВЧ-дипазона
имеет значения, равные
,
который называют углом
диэлектрических потерь.Чем
больше этот угол, тем значительнее доля
электромагнитной энергии, рассеиваемой
в в виде теплоты при протекании токов
проводимости.В справочных таблицах
обычно приводят значения тангенса
этого угла. В случае анизотропной по
отношению к электрическому полю среды
комплексная диэлектрическая проницаемость
вещества является тензором.Тангес угла
потерь хороших диэлектриков на частотах
электромагнитных колебаний СВЧ-дипазона
имеет значения, равные
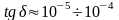 .
Если же
.
Если же
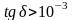 ,
то такой диэлектрик принято считать
плохим.
,
то такой диэлектрик принято считать
плохим.
3
Волновой характер переменного
электромагнитного поля. Уравнение
Гельмгольца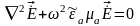 В теории волновых процессов равенство
получило название уравнения
Гельмгольца в
честь немецкого ученого Германа
Гельмгольца (1821—1894). Введем параметр
В теории волновых процессов равенство
получило название уравнения
Гельмгольца в
честь немецкого ученого Германа
Гельмгольца (1821—1894). Введем параметр
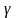 ,
в общем случае комплексный, удовлетворяющий
соотношению:
,
в общем случае комплексный, удовлетворяющий
соотношению: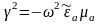 .
Далее будет показано, что
представляет собой коэффициент
распространения
плоской волны. Уравнение Гельмгольца
приобретает при этом вид:
.
Далее будет показано, что
представляет собой коэффициент
распространения
плоской волны. Уравнение Гельмгольца
приобретает при этом вид: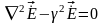 Очевидно,
что таким же окажется уравнение
относительно комплексной амплитуды
вектора напряженности магнитного поля
Очевидно,
что таким же окажется уравнение
относительно комплексной амплитуды
вектора напряженности магнитного поля
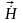
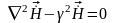 .
Таким образом, на основании уравнений
Гельмгольца (4.5) и (4.6) относительно
комплексных амплитуд векторов
напряженностей электрического и
магнитного полей можно сделать вывод
о том, что переменное
электромагнитное поле имеет волновой
характер,
т.е. оно способно распространяться в
пространстве в виде электромагнитных
волн.
.
Таким образом, на основании уравнений
Гельмгольца (4.5) и (4.6) относительно
комплексных амплитуд векторов
напряженностей электрического и
магнитного полей можно сделать вывод
о том, что переменное
электромагнитное поле имеет волновой
характер,
т.е. оно способно распространяться в
пространстве в виде электромагнитных
волн.
4 НАПРАВЛЯЕМЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ Кроме свободно распространяющихся волн, рассмотренных в предыдущих главах, существуют волны, распространение которых возможно только при наличии каких-либо направляющих элементов (границы раздела сред, металлических, диэлектрических или полупроводящих трубок, стержней и др.). Такие волны называются направляемыми.Классификация направляемых электромагнитных волн
Поперечные
волны Т-волны(ТЕМ-волны)Отсутствуют
продольные составляющие векторов
|
5 Линии передачи. Типы регулярных линий передачи
Совокупность направляемых элементов образует направляющую систему, которая служит для передачи энергии электромагнитной волны от источника (генератора) к потребителю (например, от передатчика к антенне, от приемной антенны к входу приемника и т.д.). По этой причине направляющие системы называют также линиями передачи энергии или волноводами Типы регулярных линий передачи, 1 Полые металлические волноводы2 Коаксиальные линии передачи3 Двухпроводные линии передачи4Полосковые линии передачи5Диэлектрические волноводы
6 Затухание волн в регулярных линиях передачи
Проведенный анализ общих свойств направляемых волн был выполнен в предположении, что линия передачи является идеальной, не вносит потерь. Однако на практике любые волноводы обладают затуханием, выраженным в той или иной степени. Иногда, например, при конструировании линий передачи для питания антенн или при создании дальних линий связи, затухание становится характеристикой, определяющей выбор той или иной волноводной системы. Распространение волны в реальной линии передачи сопровождается уменьшением переносимой мощности. Это связано:1) с рассеянием части мощности в металлических проводниках линии из-за конечного значения проводимости металла;2) с затуханием волны в заполняющем диэлектрике из-за существования небольших токов проводимости в диэлектрике; 3)с излучением части мощности в окружающее пространство (в линиях передачи открытого типа).
7 Критическая длина волны в прямоугольном металлическом волноводе.Области прозрачности и отсечки волновода
Длину волны
генератора, соответствующую случаю
=g,
называют критической
длиной волны
данного типа и обозначают кр.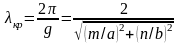 Вся область длин волн, меньших кр,
является областью «прозрачности»
данного волновода. Всю область длин
волн, которой соответствуют значения
0кр,
называют областью «непрозрачности»
или областью отсечки.
Вся область длин волн, меньших кр,
является областью «прозрачности»
данного волновода. Всю область длин
волн, которой соответствуют значения
0кр,
называют областью «непрозрачности»
или областью отсечки.
8 Критическая
длина волны и критическая частота
колебаний Е и Н типов прямоугольном
металлическом волноводе для
волн как Е-, так и Н-типов критическая
длина волны определяется одной и той
же формулой
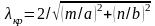 ,
Наряду с критической длиной волны можно
говорить также о критической частоте
,
Наряду с критической длиной волны можно
говорить также о критической частоте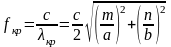 .
.
9Дисперсионная
характеристика полого металлического
волновода
Закон зависимости длины волны в волноводе
от длины волны в свободном пространстве
называют дисперсионной
характеристикой волновода.
В явном виде эта характеристика
описывается формулой, вытекающей из
выражения :
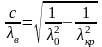 .
.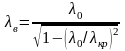 Отметим,
что вывод формулы основан лишь на двух
предпосылках – на пропорциональности
комплексных амплитуд бегущих волн
множителю
Отметим,
что вывод формулы основан лишь на двух
предпосылках – на пропорциональности
комплексных амплитуд бегущих волн
множителю
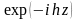 и на существовании режима отсечки.
Поскольку обе предпосылки относятся
к волне любого типа в полом металлическом
волноводе с произвольной формой
поперечного сечения, полученный здесь
результат оказывается универсальным
и может быть применим к любому волноводу.
Отличия будут состоять лишь в различных
способах вычислениях критической длины
волны.
и на существовании режима отсечки.
Поскольку обе предпосылки относятся
к волне любого типа в полом металлическом
волноводе с произвольной формой
поперечного сечения, полученный здесь
результат оказывается универсальным
и может быть применим к любому волноводу.
Отличия будут состоять лишь в различных
способах вычислениях критической длины
волны.
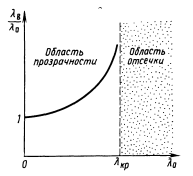 Рисунок Дисперсионная
характеристика волновода
Рисунок Дисперсионная
характеристика волновода
10Диаграмма типов
волн в прямоугольном волноводе Основной
тип волны Условие одноволновости
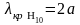 ,
,
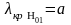 ,
,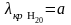 ,
,
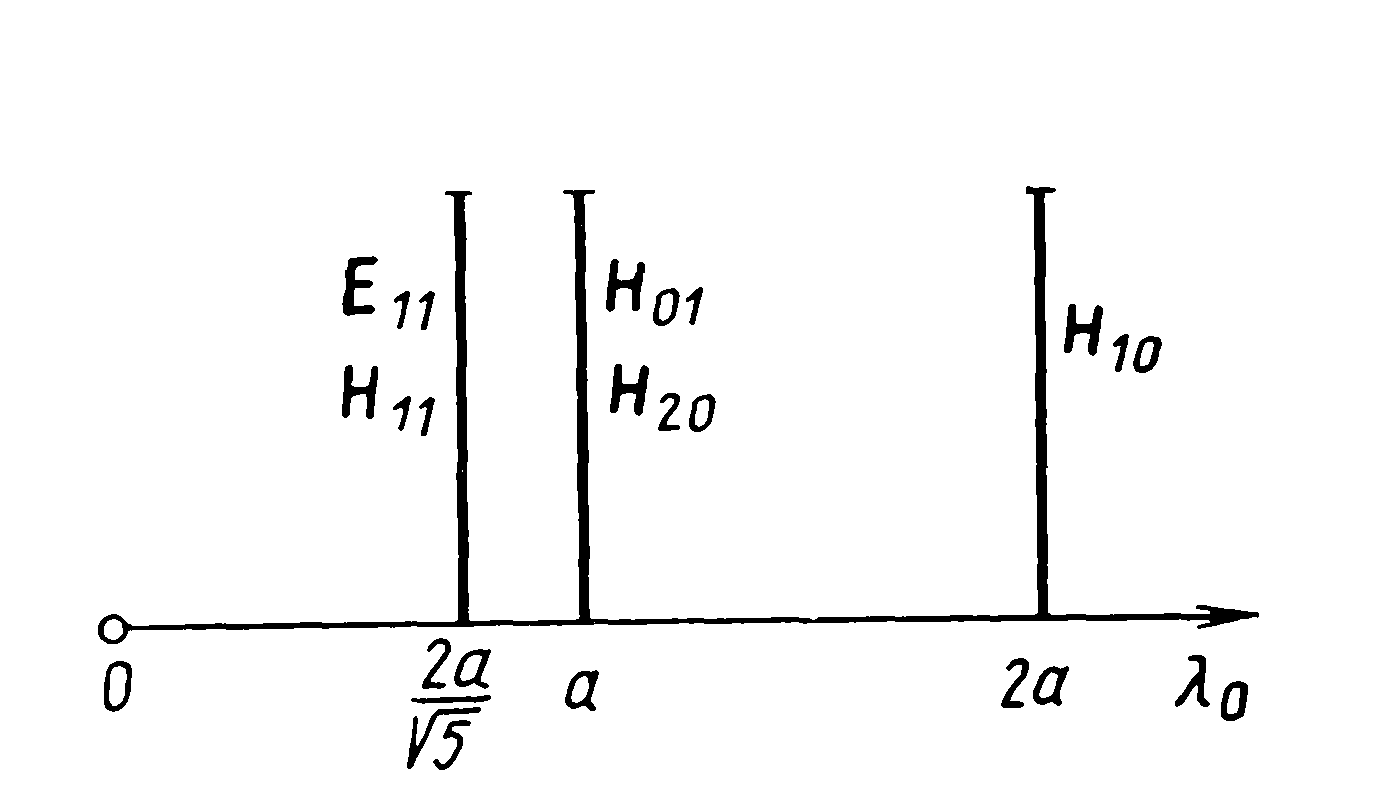
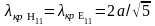 .На
основе этих вычислений построим так
называемую диаграмму
типов волн
прямоугольного волновода, -
область одноволновости (а02а),
в пределах которой может распространяться
лишь волна основного типа Н10;волна
типа
.На
основе этих вычислений построим так
называемую диаграмму
типов волн
прямоугольного волновода, -
область одноволновости (а02а),
в пределах которой может распространяться
лишь волна основного типа Н10;волна
типа
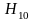 в прямоугольном металлическом волноводе
является основной,
то полученный результат формулируется
следующим образом: по прямоугольному
волноводу можно передавать колебания,
у которых длина
волны в свободном пространстве не
превышает удвоенного размера широкой
стенки волновода.
в прямоугольном металлическом волноводе
является основной,
то полученный результат формулируется
следующим образом: по прямоугольному
волноводу можно передавать колебания,
у которых длина
волны в свободном пространстве не
превышает удвоенного размера широкой
стенки волновода.

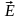 и
и
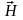 вдоль направления распространения
энергии волны
вдоль направления распространения
энергии волны