2.1 ВЫБОР СТРУКТУРЫ И РАСЧЁТ ПАРАМЕТРОВ СУЭП

За основу для разработки структуры СУЭП принимаем схему, приведённую в [1].

Рисунок 2.1 Функциональная схема СУЭП

Выбираем настройку контура скорости:

так как [1], то принимаем структуру ПИ-ПИ с настройкой на симметричный оптимум (СО).

Проверяем необходимость введения задатчика интенсивности (ЗИ) по условию [1]:

, (2.1)

где с – конструктивная постоянная ДПТ;

М_{с max} – максимальный статический момент, Н∙м.

Конструктивную постоянную находим по формуле: [1]

(2.2)

где R_я – сопротивление якорной цепи, Ом.

.

Максимальный статический момент находим по формуле:

, (2.3)

где М_сн – номинальный момент сопротивления, Н∙м.

.

Н∙м.

Н∙м.

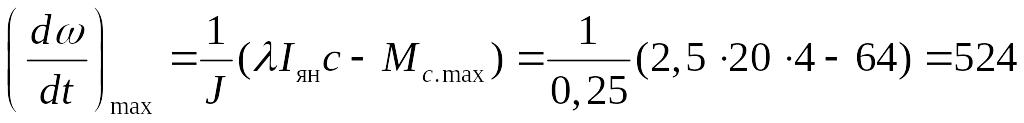с^-2.

Так как ускорение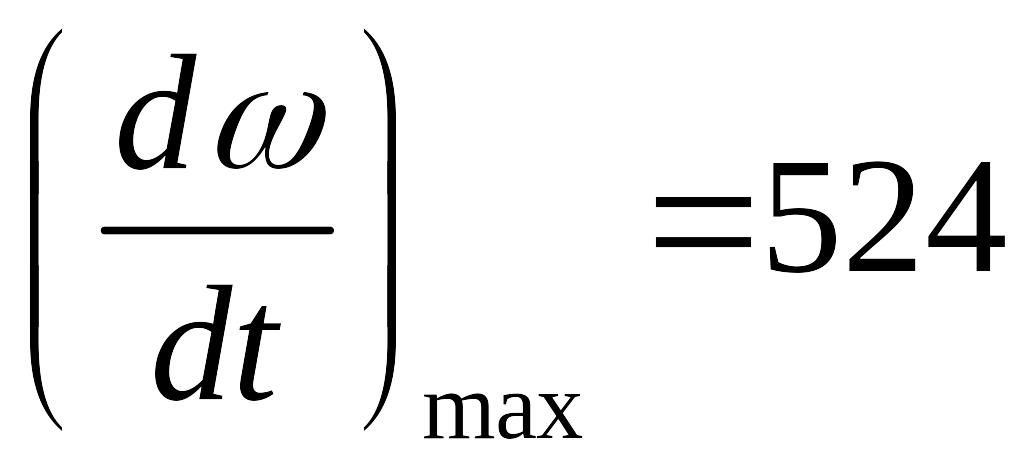 > с^-2,

следовательно применение ЗИ обязательно.

Составляем детализированную структурную схему СУЭП, принятую для моделирования динамики привода (рисунок 2.2).

Рисунок 2.2 Структура СУЭП без ЗИ.

Коэффициент К′ масштабирует входное единичное воздействие:

. (2.4)

.

Коэффициент К″ масштабирует возмущение:

.

Значение управляющего воздействия:

В.

Находим передаточную функцию (ПФ) регулятора тока [1]:

, (2.5)

где Т_яц – постоянная времени якорной цепи.

.

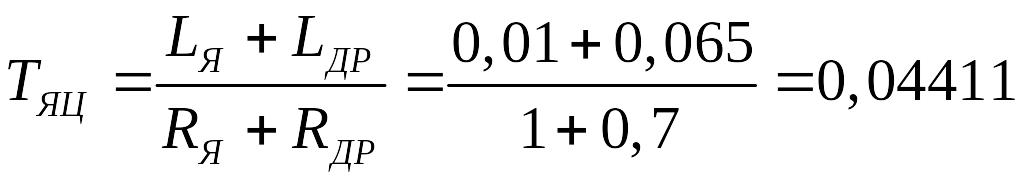с.

Найдём ПФ регулятора скорости с настройкой на СО [1]:

. (2.7)

.

Находим ПФ тиристорного преобразователя [1]:

. (2.8)

.

- передаточная функция двигателя

.

Ом – коэффициент датчика тока.

В·с – коэффициент датчика скорости.

Для нелинейных элементов (НЭ) определяем уровни ограничения. НЭ1 соответствует БОТ на рисунке 2.1. Его амплитудная характеристика показана на рисунке 2.3.

Рисунок 2.3 Амплитудная характеристика НЭ1

Для НЭ1 уровень ограничения:

. (2.9)

В.

Наличие НЭ1 позволяет ограничивать нелинейный ток якоря на уровне .

НЭ2 соответствует БОУ на рисунке 2.1. Его амплитудная характеристика показана на рисунке 2.4.

Рисунок 2.4 Амплитудная характеристика НЭ2.

Для НЭ2 уровень ограничения:

. (2.10)

.

Наличие НЭ2 позволяет ограничивать (и ) на уровне .

2.2 Структура задатчика интенсивности

Назначением ЗИ является ограничение ускорения, развиваемого приводом в переходных режимах. Структура ЗИ и характер формирования сигнала показаны на рисунке 2.5.

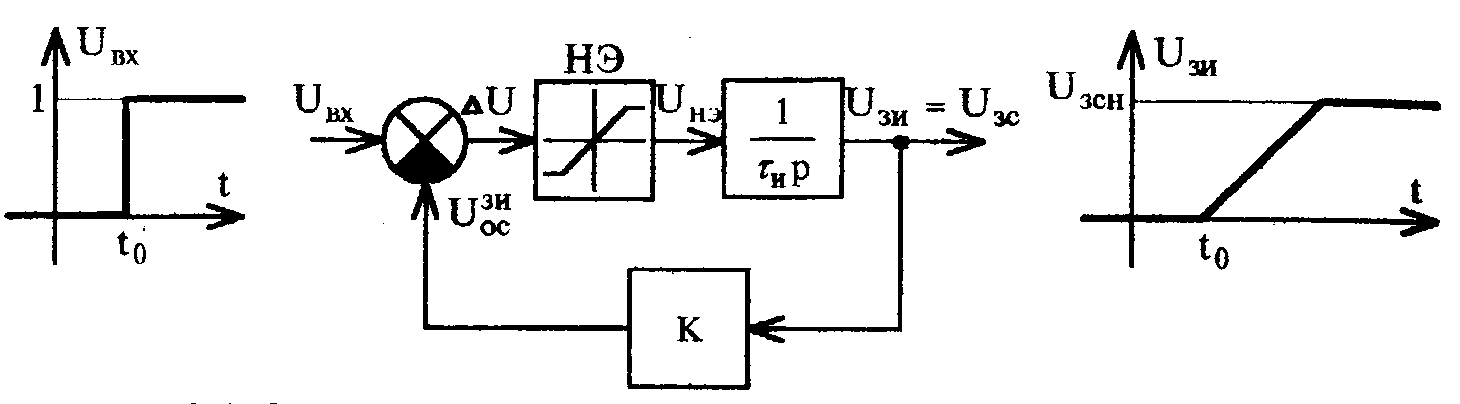
Рисунок 2.5 Структура и сигналы ЗИ.

Динамический режим ЗИ характеризуется неравенством:

. (2.11)

Практически, для нахождения скорости изменения напряжения берётся неравенство:

. (2.12)

.

В статическом режиме ЗИ при работе на номинальной скорости должно выдерживаться соотношение:

. (2.13)

Практически коэффициент k находят, положив U_вх=1, т.е. считая, что на вход ЗИ воздействует скачок 1(t):

. (2.14)

.

Амплитудная характеристика НЭ ЗИ показана на рисунке 2.6.

Рисунок 2.6 Амплитудная характеристика НЭ ЗИ.

Для НЭ задаёмся коэффициентом усиления на линейном участке k_у=75 и определяем уровень ограничения .

Значение находится с учётом выражения:

. (2.15)

Фактически, (2.15) определяет только отношение уровня ограничения к постоянной интегрирования. Поэтому задаёмся (5…12 В) и τ_и так, чтобы выполнялось равенство (2.15):

с.

.

3. Имитационное моделирование

ДИНАМИЧЕСКИХ РЕЖИМОВ ПРИВОДА

Компьютерное моделирование динамических режимов привода производим с помощью программного пакета Matlab.

За основу для разработки схемы моделирования принимается детализированная схема СУЭП (рис.2.2).

1. Моделирование переходных процессов разгона привода до номинальной скорости холостого хода в линейной СУЭП (рисунок 3.1).

Рисунок 3.1. Линейная модель

Получаем графики функций:

;

.

Полученные графики представлены на рисунках 3.2 и 3.3.

Рисунок 3.2. Зависимость .

Рисунок 3.3. Зависимость .

Проверяем правильность расчётов:

,

.

Значение перерегулирования:

,

.

Полученные значения подтверждают правильность расчётов.

2. Моделирование переходных процессов при набросе нагрузки в линейной модели (рисунок 3.1). Результатом являются графики функций:

;

.

Графики представлены на рисунках 3.4 и 3.5.

Рисунок 3.4. Зависимость

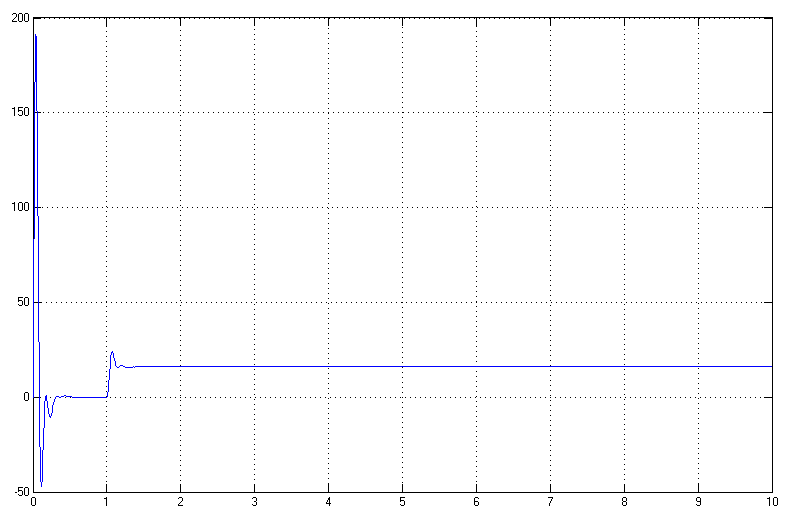
Рисунок 3.5. Зависимость

Статическая ошибка стабилизации скорости:

.

В линейной модели наблюдается большой скачок тока в момент пуска , что превышает допустимое значение .

В схему моделирования (рисунок 3.1) вводим НЭ, соответствующие БОТ и БОН(У). Производим аналогичные действия, описанные ранее.

3. Моделирование переходных процессов в нелинейной модели (рисунок 3.6). Графики переходных процессов приведены на рисунках 3.7 – 3.10. На данном этапе контролируется уровень ограничения тока якоря А.

Рисунок 3.6. Нелинейная модель

Рисунок 3.7. Зависимость .

Рисунок 3.8. Зависимость .

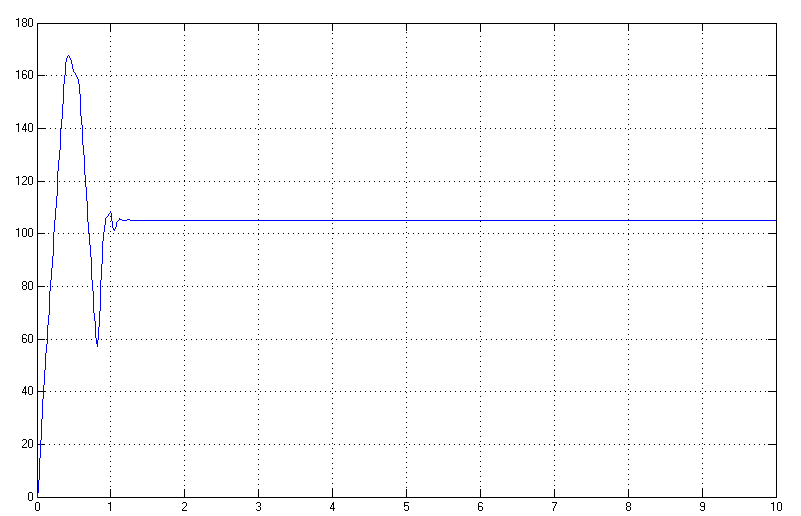
Рисунок 3.9. Зависимость .

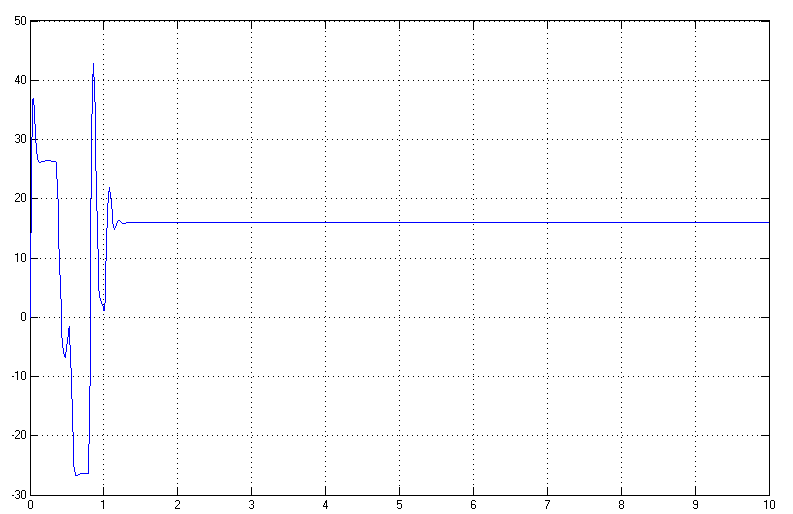
Рисунок 3.10. Зависимость .

Уровень ограничения тока якоря:

,

,

.

По полученным данным можно сделать вывод, что система отвечает требованиям проверки.

4. Моделирование переходных процессов в нелинейной модели с использованием задатчика интенсивности (рисунок 3.11). Здесь, кроме ограничения ускорения привода, на задатчик интенсивности возлагается задача масштабирования входного воздействия, поэтому коэффициент , масштабировавший в предыдущем варианте схемы входное воздействие (рисунок 3.6), из модели исключается. Графики переходных процессов представлены на рисунках 3.12 – 3.15.

Рисунок 3.11. Нелинейная модель с использованием задатчика интенсивности.

Рисунок 3.12. Зависимость .

Рисунок 3.13. Зависимость .

Рисунок 3.14. Зависимость .

Рисунок 3.15. Зависимость .

Реальное ускорение привода:

,

что не отличается от заданного ускорения более, чем на 10%.

Перерегулирование по скорости отсутствует %. Полученные данные удовлетворяют заданию