3.3. Сохранение проекта

В меню Файл выбрать Сохранить как, в появившемся окне указать путь к своей личной папке и, задав имя проекту, сохранить его.

Кроме собственно проекта полезно сохранять и снимки экрана, с тем, чтобы прикладывать их к отчету.

3.4. Отчет о лабораторной работе

Отчет о работе должен содержать титульный лист, цель и задачи работы, снимки экрана с полученными переходными характеристиками апериодического звена и выводы.

Контрольные вопросы.

1. Поясните принцип построения модели в ПК "МВТУ".

2. Что такое графический интерфейс программы?

3. Назовите основные элементы главного окна ПК "МВТУ".

4. Назовите основные вкладки Палитры блоков ПК "МВТУ".

5. Как запустить новый проект? Как открыть созданную ранее модель?

6. Как вынести блок на рабочее пространство окна модели?

7. Как соединить выход одного блока и вход другого?

8. Какая передаточная функция у апериодического звена?

9. Как выглядит переходная функция апериодического звена? Ее формула.

10. Как определить параметры апериодического звена (коэффициент усиления и постоянную времени) по его переходной характеристике?

11. Как поменять цвет кривой на виртуальном осциллографе?

12. Как изменить заголовок графика?

13. Как сохранить файл модели? Какое расширение имеет этот файл?

Лабораторная работа №2 исследование переходных процессов в типовых динамических позиционных звеньях

Цель работы: исследование переходных процессов в различных типах динамических позиционных звеньев при единичном входном воздействии.

Теоретические сведения

Типовыми динамическими звеньями называются простейшие составные части системы, поведение которых описывается обыкновенными дифференциальными уравнениями 0-2-го порядка:

(2.1)

где - входная переменная звена , -выходная переменная; -постоянные коэффициенты (параметры).

Переходным процессом называется изменение во времени переменных (сигналов) динамической системы или звена: , , обусловленное начальными условиями или входным воздействием.

Переходной функцией системы или звена y=h(t) называется переходный процесс выходной переменной при единичном входном воздействии g=1(t) (рис.2.1) и нулевых начальных условиях..

Рис.2.1

По графику переходной функции может быть определена математическая модель исследуемого динамического звена и ее параметры

Передаточные функции типовых динамических звеньев в общем случае являются произведением сомножителей:

где k, τ, T, υ, ξ - постоянные, причем k>0; υ может быть положительным и отрицательным целым числом; T>0; 0τ<1; 0ξ<1.

Перечисленные сомножители определяют различные типы динамических звеньев, среди которых выделяется подкласс позиционных, представленный в таблице 2.1. (p - оператор дифференцирования , s - комплексная величина).

Позиционные звенья, кроме консервативного, характеризуются тем, что в каждом из них при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины. Отношение установившихся значений выходной и входной величин есть передаточный коэффициент k звена.

В безынерционном (идеальном) звене при скачкообразном изменении входной величины мгновенно изменяется и выходная величина, т. е. переходного процесса нет. В апериодическом (инерционном) звене выходная величина нарастает монотонно, т. е. имеет место переходной процесс. Его продолжительность зависит от постоянной времени Т, являющейся параметром звена.

В апериодическом звене второго порядка продолжительность переходного процесса зависит от двух постоянных: Т₁ и Т₂ .

Таблица 2.1

Тип звена	Дифференциальное уравнение в операторном виде	Передаточная функция W=W(s)
Идеальное усилительное (безынерционное)	y=kx	W=k
Апериодическое (инерционное)	(Tp+1)y=kx	k W = ---------- Ts+1
Апериодическое (инерционное) второго порядка	(T22p2+T1p+1)y=kx; где T1  2T2	k k W =---------------- = -------------------, T22s2+T1s+1 (T3s+1)(T4s+1) где T3,4= 0.5 (T1T12-4T22)
Колебательное	(T2p2+2Tp+1)y=kx, где 0<<1	k W = ----------------- T2s2+2Ts+1
Консервативное	(T2p2+1)y=kx;	k W = ---------- T2s2+1

Апериодическое звено второго порядка также можно представить как последовательное соединение двух апериодических звеньев первого порядка.

Выходная величина колебательного звена в переходном процессе колеблется около того значения, которое должно установится. Затухание колебаний зависит от коэффициента демпфирования . Точнее, скорость затухания характеризуется коэффициентом затухания =/T.

У гловая частота колебаний  = 1-²/Т.

Консервативное звено есть частный случай колебательного звена (=0) и характеризуется незатухающими колебаниями при постоянном воздействии на входе.

Во временной области переходные характеристики описываются выражениями, представленными в таблице 2.2.

Таблица 2.2

N	Тип звена	Переходная характеристика h = h(t)
1	Идеальное усилительное (безынерционное)	h = k
2	Апериодическое (инерционное)
3	Апериодическое (инерционное) второго порядка
4	Колебательное	.
5	Консервативное

Амплитуда первого положительного выброса переходного процесса в колебательном звене определяется выражением

. (2.1)

А амплитуда первого отрицательного ₂ выброса связана с ₁ отношением

. (2.2)

При ξ > 1 трение в системе, рассеивание энергии, относительно велико и колебательность переходной функции исчезает, функция становится монотонной.

Постоянная времени Т колебательного звена не равна периоду колебаний Т_кол, она связана с периодом, но существенно меньше его:

при ξ < 0.5 период затухающих колебаний примерно равен Т_кол ≈ 2 π Т.

По колебательной переходной характеристике звена можно приближенно оценить его параметры (рис 2.2):

• уровень успокоения колебаний равен коэффициенту усиления k звена;

• постоянная времени приближенно равна Т ≈ Т_кол / 2π

• декремент затухания ξ ≈ 3Т / Т_пер, где Т_пер - длительность переходного процесса, определяемая промежутком времени, за которое переходная функция попадает в пятипроцентный коридор.

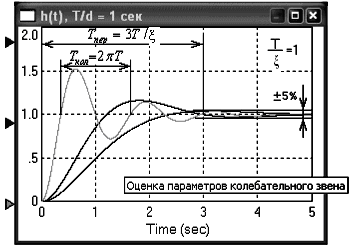
Рис. 2.2. Переходные характеристики колебательного звена

Выполнение лабораторной работы

1. В соответствии с вариантом, указанным преподавателем, выбрать из таблицы 2.3 параметры исследуемых звеньев.

Таблица 2.3

№	Па	Варианты
звена	ра-метр	1	2	3	4	5	6	7	8	9	10
1	k	1 4	2 5	3 7	4 9	1 5	2 6	2 7	3 8	4 9	6 10
2	T	0.01 0.03	0.02 0.06	0.03 0.09	0.04 0.12	0.05 0.15	0.06 0.18	0.07 0.21	0.08 0.24	0.09 0.27	0.1 0.3
3	Т1	2 3	4 2	6 3	8 4	9 5	6 6	7 7	8 8	9 9	4 6
	Т2	1 1	2 1	3 1	4 2	4 2	2 3	3 2	4 3	4 3	2 2
	k	1	2	3	4	5	6	7	8	9	10
4	T	0.01 0.03	0.02 0.06	0.03 0.09	0.04 0.12	0.05 0.15	0.06 0.18	0.07 0.21	0.08 0.24	0.09 0.27	0.1 0.3
		0.1 0.01	0.2 0.002	0.3 0.03	0.4 0.04	0.5 0.05	0.6 0.06	0.7 0.07	0.8 0.08	0.9 0.09	0.55 0.078

Примечание: для звеньев 2 и 3 коэффициент k соответствует значениям для звена 1. Для звена 5 параметры k и T соответствуют значениям для звена 4.

2. С помощью программного комплекса МВТУ синтезировать схемы исследования и провести эксперимент для входного воздействия в виде единичной ступенчатой функции.

Для звена 2 одному из значений коэффициента k соответствуют оба значения параметра Т.

Для звена 3 реализуются два сочетания параметров Т₁ и Т₂.

Для звена 4 - два сочетания параметров T и . Конечное значение модельного времени выбирается таким, чтобы переходной процесс успел установиться.

2. Получить графики выходной величины для каждого звена при указанных параметрах входного воздействия.