- •Министерство образования и науки рф
- •Иркутский государственный технический университет физическая и коллоидная химия
- •260200 Производство продуктов питания
- •Иркутск 2012
- •Общие методические указания
- •Ниже приводится краткий консультативный материал в качестве помощника усвоения указанных тем Теплоемкость
- •Занятие 2.
- •2. Каталитические реакции
- •Далее приводится краткий консультативный материал в качестве помощника усвоения указанных тем
- •Исходные данные
- •Математическая обработка экспериментальных данных. Интегрально-расчетный метод
- •Математическая обработка экспериментальных данных.
- •Далее приводится краткий консультативный материал в качестве помощника усвоения указанных тем.
- •4. Агрегативная устойчивость
- •Далее приводится краткий консультативный материал в качестве помощника усвоения указанных тем.
- •Лекции семестра №4 Лекция 1
- •Раздел 1. Химическая термодинамика.
- •Тема 1.1. Законы термодинамики (исп. Видеофильм и слайд-лекция)
- •Лекция 2 Первое начало термодинамики
- •Работа расширения идеального газа в различных процессах
- •Лекция 3 Термохимия
- •Теплоемкость
- •Приближенные методы расчета теплоемкости
- •Зависимость теплоемкости от температуры
- •Лекция 4
- •Стандартное состояние вещества
- •Лекция 4 второе начало термодинамики. Энтропия
- •Статистическая интерпретация энтропии
- •Лекция 5 третье начало термодинамики
- •Термодинамические потенциалы
- •Лекция 6 химическое равновесие
- •Лекция 7
- •Лекция 8-10 фазовые равновесия (диаграммы двух и трёхкомпонентные на слайд-лекциях)
- •Лекция 11 Термодинамика растворов (слайд-лекции)
- •Образование растворов. Растворимость
- •Л екция 12 Растворимость твердых веществ в жидкостях
- •Лекция 13
- •Лекция 14
- •Лекция 15
- •Лекция 16
- •Лекция 17 электрохимические процессы
- •Лекция 18
- •Лекция 19 химическая кинетика
- •Лекция 20
- •Лекция 21
- •Лекция 22
- •Лекция 23
- •Лекция 24
- •Лекция 25 Коллоидная химия Адгезия, смачивание и растекание
- •Лекция 26 Адсорбция
- •Лекция 27
- •Лекция 28
- •Лекция 29
- •Лекция 30
- •Лекция 31
- •Лекция 32
- •Лекция 33
- •Лекция 34
- •Лекция35
- •Формы контроля по дисциплине и оценка качества подготовки
- •Литература
Исходные данные
Время, τ, мин |
0 |
12,8 |
30 |
47 |
68 |
800 |
100 |
∞ |
Концентрация продукта, с∙103, моль/л |
0,0 |
3,0 |
7,0 |
10,3 |
11,4 |
13,0 |
13,7 |
14,0 |
Решение:
Рассчитаем
концентрацию исходного реагента
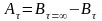 ,
,
где
 – текущая концентрация исходного
реагента;
– текущая концентрация исходного
реагента;
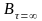 –
предельная концентрация продукта
реакции;
–
предельная концентрация продукта
реакции;
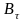 –
текущая концентрация продукта (табл.
8).
–
текущая концентрация продукта (табл.
8).
Интегрально-расчетный метод
Пусть n= 0. Тогда константу скорости реакции рассчитаем по уравнению:
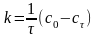 ,
,
где
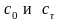 –
начальная и текущая концентрации
реагента.
–
начальная и текущая концентрации
реагента.
Константа скорости реакции по результатам расчетов не усредняется (табл. 2). Следовательно, порядок реакции не равен нулю.
Таблица 2
Математическая обработка экспериментальных данных. Интегрально-расчетный метод
№ пп |
Время, τ, мин |
Концентрация продукта, с∙103, моль/л |
Концентрация исходного вещества, с∙103, моль/л |
п = 0
моль/л∙мин–1 |
п = 1
мин-1 |
1 2 3 4 5 6 7 8 |
0 12,8 30 47 68 80 100 ∞ |
0,0 3,0 7,0 10,3 11,4 12,5 13,0 14,0 |
14,0 11,0 7,0 3,7 2,6 1,5 1,0 0 |
- 2,344∙10-4 2,333∙10-4 2,190∙10-4 1,700∙10-4 1,563∙10-4 1,390∙10-4 - |
- 1,90∙10-2 2,31∙10-2 2,83∙10-2 2,48∙10-2 3,16∙10-2 2,64∙10-2 - |
Пусть
n= 1.
В этом случае константу скорости реакции
рассчитаем по уравнению:
 .
.
Расчет
константы скорости показывает, что ее
значение можно усреднить
 мин-1
(табл. 2), следовательно, реакция первого
порядка.
мин-1
(табл. 2), следовательно, реакция первого
порядка.
Интегрально-графический метод заключается в подборе ординаты для зависимости концентрации от времени.
Пусть
n = 0.
Используем уравнение прямой линии:
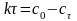 или
или
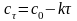 и строим график (рис.1). Видно, что
экспериментальные точки находятся на
кривой второго порядка и не укладываются
на прямую. Следов
и строим график (рис.1). Видно, что
экспериментальные точки находятся на
кривой второго порядка и не укладываются
на прямую. Следов ательно,
реакция не нулевого порядка.
ательно,
реакция не нулевого порядка.
Для
дальнейшего исследования используем
уравнение прямой линии
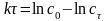 или
или
 .
Зависимости в координатах lnсτ
= f(τ) будет
линейна (рис. 2).
.
Зависимости в координатах lnсτ
= f(τ) будет
линейна (рис. 2).
Следовательно, данная реакция первого порядка. Константу скорости найдем по тангенсу угла наклона прямой к оси абсцисс:
 =
k
=
k
Дифференциально-расчетный метод
Рассчитаем
средние скорости и соответствующие им
средние концентрации за периоды времени
от
 до
до
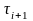 (i=1,2,…7)
по выражениям:
(i=1,2,…7)
по выражениям:
 и
и
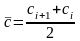 ,
а затем определим ni
и ki
по формулам
,
а затем определим ni
и ki
по формулам
 и
и
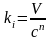 .
Результаты расчетов сведем в табл. 3.
.
Результаты расчетов сведем в табл. 3.
Таблица 3
Математическая обработка экспериментальных данных.
Дифференциально-расчетный метод
№ п/п |
τ, мин |
с∙103, моль/л |
моль/л∙мин–1 |
моль/л |
|
|
пi |
k∙102 мин–1 |
1 2 3 4 5 6 7 8 |
0 12,8 30 47 68 80 100 ∞ |
14,0 11,0 7,0 3,7 2,6 1,5 1,0 0 |
2,3440 2,3260 1,9412 0,5240 0,9170 0,2500 |
12,50 9,00 5,35 3,15 2,05 1,25 |
0,00335 0,07854 0,56874 -0,2430 0,56443 |
0,143 0,226 0,230 0,185 0,215 |
0,025 0,350 2,470 -1,30 2,630
|
1,875 2,584 3,630 1,664 4,473 2,000
|
О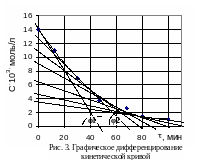 бщий
порядок реакции равен среднеарифметическому
значению
ni:
бщий
порядок реакции равен среднеарифметическому
значению
ni:
 или
или
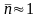 .
Усредненное значение константы скорости
.
Усредненное значение константы скорости
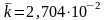 .
.
Дифференциально-графический метод
Строим
график зависимости в координатах
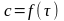 (рис. 3).
(рис. 3).
Из
графика следует найти скорости и
концентрации, являющимися параметрами
основного кинетического уравнения:
 .
Для этого дифференцируем кривую на
графике методом касательных и находим
тангенс угла наклона каждой касательной
линии к оси абсцисс: –
.
Для этого дифференцируем кривую на
графике методом касательных и находим
тангенс угла наклона каждой касательной
линии к оси абсцисс: –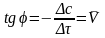 .
Среднюю концентрацию находим из графика,
разделив отрезки, отсекаемые касательными
на оси ординат, пополам, либо находим
полусуммы двух соседних концентраций
в точках пересечения касательных с осью
ординат. В нашем примере тангенсы угла
наклона φ1
и φ2
найдем из следующих выражений:
.
Среднюю концентрацию находим из графика,
разделив отрезки, отсекаемые касательными
на оси ординат, пополам, либо находим
полусуммы двух соседних концентраций
в точках пересечения касательных с осью
ординат. В нашем примере тангенсы угла
наклона φ1
и φ2
найдем из следующих выражений:
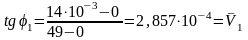



и т.д. (табл. 4).
Таблица 4


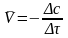 ∙104
∙104 ∙103
∙103