Термодинамические потенциалы

Изменение энтропии определяет направление процесса лишь в изолированных системах. Однако на практике больший интерес вызывают системы, обменивающиеся с окружающей средой энергией (закрытые системы). Поэтому, для характеристики этих процессов были введены термодинамические функции – свободная энергия Гельмгольца (изохорно-изотермический потенциал) и свободная энергия Гиббса (изобарно-изотермический потенциал). Для сокращенного названия принято определение: энергия Гельмгольца (F, Дж, кДж, Дж/моль, кДж/моль) и энергия Гиббса (G, Дж, кДж, Дж/моль, кДж/моль).

«Поведение» термодинамической системы характеризуют энтальпийный и энтропийный факторы. Энтальпийный фактор отражает стремление системы к минимуму «тепловой энергии»; энтропийный – отражает стремление системы к максимальной неупорядоченности. Например, для изолированных систем (при ΔН = 0) критерий направленности самопроизвольного процесса, а также предел его протекания определяется величиной изменения энтропии (ΔS). Если система находится при температурах, близких к абсолютному нулю, то критерием направленности является изменение энтальпии, т.к. в этом случае энтропия не изменяется или равна нулю.

Для закрытых систем при температурах, не равных нулю, при определении направленности процесса, необходимо учитывать оба фактора. Поэтому в любых системах направление и предел протекания самопроизвольного процесса определяет более общий принцип минимума свободной энергии:

Самопроизвольно могут протекать только те процессы, которые приводят к понижению свободной энергии системы; система приходит  в состояние равновесия, когда свободная энергия достигает минимального значения.

Для закрытых систем, находящихся в изобарно-изотермических либо изохорно-изотермических условиях свободная энергия принимает вид изобарно-изотермического либо изохорно-изотермического потенциалов (т.н. свободная энергия Гиббса и Гельмгольца соответственно). Данные функции называют иногда просто термодинамическими потенциалами, что не вполне строго, поскольку термодинамическими потенциалами являются также внутренняя энергия (изохорно-изоэнтропийный) и энтальпия (изобарно-изоэнтропийный потенциал).

Рассмотрим закрытую систему, в которой осуществляется равновесный процесс при постоянных температуре и объеме (V, T = const). Выразим работу данного процесса, которую обозначим A_max (поскольку работа процесса, проводимого равновесно, максимальна), из уравнений (53, 54).

Запишем уравнение первого начала термодинамики для дифференциально малого количества теплоты Из второго начала

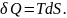
Подставим TdS в уравнение первого начала и решим его относительно δА:

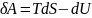  (68)

или после интегрирования от S₁ до S₂ и от U₁ до U₂:

  (69)

Преобразуем выражение (69), сгруппировав члены с одинаковыми индексами:

  (70)

Введя обозначение:

(71)

получаем:

  (72)

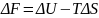(73)

Функция  есть изохорно-изотермический потенциал (свободная энергия Гельмгольца), определяющий направление и предел самопроизвольного протекания процесса в закрытой системе, находящейся в изохорно-изотермических условиях. 

Закрытую систему, находящуюся в изобарно-изотермических условиях, характеризует изобарно-изотермический потенциал G:

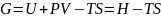  (74)

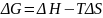  (75)

Поскольку –ΔF = A_max, можно записать:

(76)

Величину А'_max называют максимальной полезной работой (максимальная работа за вычетом работы расширения). Основываясь на принципе минимума свободной энергии, можно сформулировать условия самопроизвольного протекания процесса в закрытых системах.

Условия самопроизвольного протекания процессов в закрытых системах:

Изобарно-изотермические  (P = const, T = const):

ΔG < 0,          dG < 0

Изохорно-изотермические (V = const, T = const):

ΔF < 0,           dF < 0

Процессы, которые сопровождаются увеличением термодинамических потенциалов, протекают лишь при совершении работы извне над системой. В химии наиболее часто используется изобарно-изотермический потенциал, поскольку большинство химических (и биологических) процессов происходят при постоянном давлении. Для химических процессов величину ΔG можно рассчитать, зная ΔH и ΔS процесса, по уравнению (75), либо пользуясь таблицами стандартных термодинамических потенциалов образования веществ ΔG°_обр; в этом случае ΔG° реакции рассчитывается аналогично ΔН° по уравнению 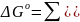(77):

  (77)

Величина стандартного изменения изобарно-изотермического потенциала в ходе химической любой реакции есть мера химического сродства исходных веществ. Основываясь на уравнении (75), можно оценить вклад энтальпийного и энтропийного факторов в величину ΔG и сделать некоторые обобщающие заключения о возможности самопроизвольного протекания химических процессов, основываясь на знаке величин ΔН и ΔS.

1. Экзотермические реакции; ΔH < 0.

а) Если ΔS > 0, то ΔG всегда отрицательно; экзотермические реакции, сопровождающиеся увеличением энтропии, всегда протекают самопроизвольно.

б) Если ΔS < 0, реакция будет идти самопроизвольно при ΔН > TΔS (низкие температуры).

2. Эндотермические реакции; ΔH > 0.

а) Если ΔS > 0, процесс будет самопроизвольным при ΔН < TΔS (высокие температуры).

б) Если ΔS < 0, то ΔG всегда положительно; самопроизвольное протекание эндотермических реакций, сопровождающихся уменьшением энтропии, невозможно.