Условные и безусловные знп
Если в системе или в уравнении отсутствует ограничения, то задача наз-ся з-чей безусловной оптимизации.
Безусловная задача решается легче,чем условная з-ча, поэтому наряду с прямым методом решения услов задач часто применяется метод преобразования условных задач в бузуслов оптимизации, путем введения штрафных ф-ций.
метод
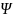– преобразования
является одним из эффективных методов, позволяющих решать много задач оптимизации (найти глобальный экстремум).
сущность
метода: объект исследования и анализа
не сама ц.ф., а некоторая другая функция
Ψ(L),
образуемая в результате преображения
ф. f(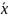
)
если
ц.ф. . f(
)
является измеримой определенной на
некотором множестве Е’ R’’
пространства и не терпящий симметричн.
разрыва 1-ого рода, то
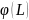является монотонно убывающей и ноль
этой функции соотвествует значению
max
ц.ф. f(
)
Метод штрафных функций
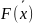=f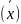
+
-
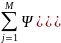безусловная задача оптимизации
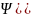-штрафная
ф-ия, путем добавления к целев. ф-ии
одной или нескольких функций, учитывающие
ограничения. Все условия учитываются
в штраф. ф-иях.
В
кач-ве штраф. ф-ии можно взять функцию
,
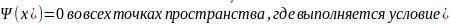
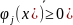и
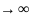если это условие не выполняется.Поэтому
если все условия выполняются , то min
совпадает, а если не вып-ся, то добав шт
ф-ций.
Алгоритм
решения задачи min
f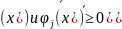
,
с использов шт ф-ций.
1)
выбир нач точку
,в
данной точке
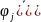)>0,
2)
при k=1,2,3,...,
начиная с точки
)
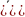решается задача безусловной оптимизации,
в результате определяется очередная
точка
)
)
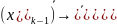и т. д. процесс повторяется.
Если
на каждом шаге алгоритма удается найти
глобальн min
ф-цию
)
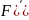по x,
то последовательность
)
сойдется к глобальн min-му
ф-ции f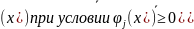
при
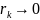
Обычно
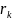выбирают:
/
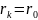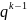причем q>1-
const,
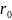=[50;100]
примечание . Если решается max(min)
{ аналогич. образом строятся шт. ф-ции , причем по отдельности для условий типа равенства и неравенства.
Метод Гомори. Целочисленное решение
Значительная часть задач коммерческой деятельности требует целочисленного решения. К ним относятся задачи, у которых переменные величины означают количество единиц неделимой продукции, например распределение товаров между коммерческими предприятиями, раскрой материалов, число станков при загрузке оборудования, распределение транспортных средств по рейсам, распределение коммерческих заказов между оптовыми предприятиями, продажа автомобилей, распределение самолетов по авиалиниям, количество вычислительных машин в управляющем комплексе и др. Линейные задачи, решение которых должно быть получено в целых числах, называют задачами целочисленного программирования. Задача целочисленного программирования формулируется так же, как и задача линейного программирования, но включает дополнительное требование, состоящее в том, что значения переменных должны быть целыми неотрицательными числами, например, х1 = 30 станков, х2 = 16 самолетов, х3= 7 человек. Методы целочисленной оптимизации можно разделить на три основные группы: а) методы отсечения; б) комбинированные методы; в) приближенные методы. Рассмотрим один из методов отсечения — метод Гомори. Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами: а) оно должно быть линейным; б) должно отсекать найденный оптимальный нецелочисленный план; в) не должно отсекать ни одного целочисленного плана. Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением. Алгоритм Гомори, основанный на симплексном методе, имеет простой способ построения правильного отсечения и содержит следующие этапы. 1. Задача линейного программирования решается без учета условия целочисленности симплексным или двойственным симплексным методом. Если все элементы оптимального плана целые числа, то решение заканчивается для задачи целочисленного программирования. 2. Если среди элементов оптимального решения есть нецелые числа, то необходимо выбрать элемент с наибольшей дробной частью и составить дополнительное ограничение (сечение), которое отсекает нецелочисленные решения. Дополнительное ограничение дается в том случае, если значение базисной переменной в оптимальном плане xi=bi — дробное число. Тогда некоторые элементы аij в i-й строке симплексной таблицы также дробные числа. Обозначим [bi] и [аij] целые части чисел bi и аij, т.е. наибольшие целые числа, не превышающие bi и aij. Величины дробных частей qi и qij определяются как разности следующим образом: qi = bi - [bi]; qij =аij - [aij] и являются положительными числами. Тогда неравенство qi-qi1 x1 - qi2x2 - ... - qimxn 0, сформированное по i-й строке симплексной таблицы обладает всеми свойствами правильного отсечения. 3. Неравенство преобразуется в уравнение путем введения дополнительной неотрицательной переменной и включается в оптимальную симплексную таблицу. 4. Полученная расширенная задача решается двойным симплексным методом. Если новый оптимальный план будет целочисленным, то задача решена. В противном случае необходимо вернуться к п. 2 алгоритма. Если в процессе решения в симплексной таблице появится уравнение с нецелым свободным членом bi и целыми коэффициентами aij, то данная задача не имеет целочисленного оптимального решения. Пример. Маркетинговые исследования указали на необходимость освоения выпуска новой продукции. Поэтому на предприятии решено установить новое технологическое оборудование на освободившейся площади 10 м2. На приобретение оборудования двух видов выделено 6 млн. руб. Комплект первого вида оборудования стоимостью 1 млн руб. устанавливается на площади 5 м2 и позволяет увеличить доход предприятия на 8 млн руб. Комплект второго вида оборудования занимает площадь 2 м2, стоит 1 млн руб. и обеспечивает увеличение дохода предприятия на 5 млн руб. Определите, какое количество технологического оборудования каждого вида следует закупить, чтобы обеспечить максимальное увеличение дохода предприятия от продажи выпускаемой продукции. |