
- •Градиентные методы. Метод наискорейшего спуска
- •Метод наискорейшего спуска
- •Задачи лин и нелин программирования
- •Задача дискретного программирования
- •Знп и методы его решения
- •Условные и безусловные знп
- •Метод штрафных функций
- •3 Алгоритм гомори
- •Методы сканирования.Случ поиска м-д Нельдера-Нида.
- •Априорные процедуры
- •Линейная свертка
- •Принцип справедливого компромисса
- •Выделение глав. Критерия
- •Принцип гарантированного результата
Градиентные методы. Метод наискорейшего спуска
Применение
класс. методов Мат. анализа для нахождения
экстремума целев. ф-ции сопряжено
большими трудностями.1) только необходимо
условие экстремума:
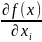 =0
=0
2) приходиться решать систему нелинейных уравнений
3) экстремум может нах-ся на границе области.
Эффективным м-дом решения ЗНП яв-ся градиентный метод. Градиент – вектор направленное по нормали к поверхности постоянного уровня, где выполняется условие.
f(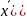 =
const
с алгебраической величиной, равной
=
const
с алгебраической величиной, равной
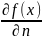 ,
где n-
нормаль к поверхности пост. уровня.
,
где n-
нормаль к поверхности пост. уровня.
grad
f(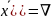 f(
=
(
f(
=
(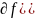 ,
)
,
)
Градиент по направлению совпадает с направлением наискорейшего возрастания целевой функции f( , т.е. это кратчайший путь к max f( , и наоборот.
Благодаря этому способу градиент примен-ся для решения ЗНЛП. Алгоритм град м-да может быть записан след. обр.Градиент- обычно для решения безусловных задач оптимизации.Рабочая формула имеет вид:
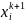 =
=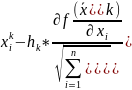
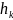 -
шаг спуска(параметр)
-
шаг спуска(параметр)
Есть
простая формула:
= *
*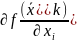 ,
,
где
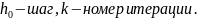
Условия окончания когда выполняется условие
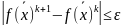
Метод наискорейшего спуска
Это тоже град метод .Выбирается начальная точка , в кот вычисляется град и по данному направлению совершается движение (шаг), т.е. спуск или подъем.Если есть улучшение, то продолжаем движение в том же направлении.Т.о. нашли след точку , в кот вычисляется град-т и продолж-ся аналогичное движение пока не найдем оптимум.Данный метод быстрее приводит к оптимуму.
Безградиентные методы
существует гр. безградентных методов, которые в процессе нахождения экстремума использует и информацию, получаемые от сравнительного анализа значений целевой функции в различных точках ( в результате очередного шага).
безград. методы исп-ют производ. методы:
Метод сканирования. Суть: последний просмотр значений целевой функции в ряде точек, принадлежащих допустимой области и нахождение среди них точек, в которых достигается экстремум целевой функции.

0сн. достоинство метода: при достаточно «густом» расположении удается найти глобальный экстремум.
недостаток: много точек - много вычислений.
Модифицированный метод. сканирования. применяется чаще на практике. р-н разбивается на мелкие шаги.
Симплекс-метод (Кельдера-Нида) .
осн. идея закл. в след.: по известным значениям целевой функции в вершинах выпуклого многогранника, называемого симплексом, определяется направление, в котором требуется сделать очередной шаг, чтобы получить наиб. уменьшение (увеличение) ц.ф.
схема поиска при этом основана на слежении за изменением значений значений ц.ф. в вершинах симплекса (тетраэдр – 3хмерн).
главный здесь является отражение – процесс нахождения вершины нового симплекса, расположенного симметрично относительно плоскости, проходящей через одну из сторон исходного симплекса.
выбор направления поиска вершины нового симплекса определяется положением той вершины исходного симплекса, в котором ц.ф. имеет наихудшее значение (если min, то большое значение).
новая точка называется дополнением наихудшей точки если есть улучшение значения нового точки для нового симплекса. если нет улучшения, возвращается в исходный симплекс и находим следующую по значению наилучшую точку.
все сводится к нахождению координат нов. точки. решается задача безусловной оптимизации.
есть модифицированный симплекс-метод, в котором процесс нахождения нов. величины в сторону симплекса или сжимается или растягивается. это есть метод нельдера-нида.
Метод случайного поиска
согласно этому методу: перебор случ. значений независим. переменных найти оптимум и ц.ф. или направление к нему.
а) «слепой поиск»: из допустимой области берется случ. точка Ха, вычисляется в ней значение функции , далее берем след. случ. точку . значения в двух точках сравниваем и записываем где лучше. далее очередную точку до тех пор, пока не найдем оптимум.
б) метод случ. направлений
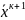 =
=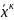 + h
+ h
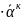
к=0,1,2,3...
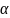 -
случ. вектор
-
случ. вектор
h – const (парметр)
