
Шпоры.Диффуры.3 сем
.docx
|
Доказательство: 1(x)…n(x)- реш., C1…Cn: C11+…+Cnn – реш. Пусть y(x) – произвольное решение системы (1). Зафиксируем x0I. Вычислим y(x0)= y0. Вычислим 1(x)…n(x)- они лин. незав., т.к. W(x0)0. Числа y0, 1(x0)…n(x0) Rn(Cn), значит: y0 лин. выражается 1(x)…n(x), т.е. сущ. 1…n такие, что y0=i=1nii(x). Рассм. вект.-функц. Z(x)= y(x) - i=1nii(x). Z(x) – решение сист. (1). Z(x0)= y(x0) - i=1nii(x0)= y0 - i=1nii(x0)=0. Таким образом Z(x) – решение зад. Коши dy/dx=A(x)y, y(x0)=0. Эта задача имеет только нул-ое реш. xI: Z≡0, т.е. y(x)=i=1nСii(x). |
|
|
|
Докзательство:
Из
теор (11) (_Для
того чтобы вектор-функция y=γeλx
являлась решением системы
Действ.случ: A = ||aij||nn, ij: aijR; (3) dy/dx = Ay (4) det|A - E| = 0 – действ. многочлен. степ. n и урав. имеет корни 1… n. I) Пусть 1… n-прост. действ. корни.( т.е. i≠j, j≠i); тогда сист. (3) имеет ФСР y1=γ1*e1x… yn=γn*enx; где γ1…γn-дейст.соб.век. Общ.реш.: C1γ1e1x+…+ Cnγnenx
II)
Пусть
среди 1…
n
встреч. компл. числа =
+ i,
, ex= e( + i)= ex(cosx+i*sinx) e(сопряж)x= e( - i)= ex(cosx-i*sinx), след. ex(сопряж)= e(слпряж)x |
Необходимо: L[ψ(x)]= b(x) Подставляем ψ(x) в (9)
Ψ= dψ/dx=A(x) ψ(x)+b(x)
dψ/dx=
+b(x)=
Заметим,
= Получим
систему:
Ф(x)= С(x)=(
det
Ф(x)=W(x)=W[
Ф(x)C’(x)=b(x), C’(x)=Ф-1(x)b(x)=g(x) Ci’(x)=gi(x) i=1,…n
Ci(x)=
y=
ψ+
y=
k1, … kn – произвольные постоянные
|
|
|
33.Следствие
1. Все решения
системы ЛДУ устойчивы (ассимтотически
устойчивы), если у этой системы
Следствие
3. Система
ЛДУ называется (асимтотически)
устойчивой, если у нее
Замечание.
1) вектор-функция
2)
3)Если
Теорема 2. Система ЛДУ устойчива т и тт, когда все решения этой системы ограниченны (без док-ва) |
32.Решение y(t,y0*) неустойчиво, если: 1.выполняется 2.
*для одной и той же системы одно решение может быть устойчивым, а другое неустойчивым. Сведение к исследованию на устойчивость нулевого решения приведенной системы. Пусть дана задача Коши (1),(2). Исследуем на устойчивость реш (1),(2*). y=y(t,y0), введем новую переменную x(t) = y(t)-y(t,y0*), y(t) – произвольное решение (1) Сделаем замену в задаче (1),(2)
y=y(t,y0) решение
(1),(2*) т.е
y(t0,y0*)=y0*,
y(t)=x(t)+y(t,y0*)
x(t)
Обозначим: f(t,x)=F(t,x(t)-y(t,y0*)-F(t,y(t,y0*))) Приведенная задача: (1’)
(2’) y(t,y0)
– устойчивость(асимптотическая
устойчивость) решения x
|
31.Теор. 2.: Пусть lÎС и `l комплексно-сопряж . Если y=γeλx , где γЄ Cn явл-ся реш-ем с-мы(3), то ф-я `y(x) также явл-ся реш-ем с-мы (3). При этом, если y(x)=U(x)+iV(x) , где U(x), V(x) действит вектор-ф-ции, то U(x) и V(x) также реш-е с-мы (3). Док-во:` y=` γ` eλx =` γ e`λx ; согласно теор 1 явл-ся реш (3) т и т т когда λ явл-ся собст значением матр А а γ¹`0 соб вектор удовлет соб знач-ю λ, т е А γ= λ γ ; `А` γ=` λ` γ ; значит А γ=` λ `γ т е `λ – собст значение матр А, `γ-собст вектор приним собст знач `λ . По теор 1 в этом случае `y= γ e`λx явл решением сист (3) Предст y(x)=U(x)+iV(x), где U(x) и V(x) действит вект ф-ия. По теор 3, если y(x) явл-ся реш сист (3), то U(x)=Rey(x) и v(x)=Jmy также реш с-мы (3) Лемма:
Если
y1(x),
Док-во: y1(x),…yn(x) – ФСР, то W(0)=0, W(o)=W(U(x)+iV(x),U(x)-iV(x),y3(x),…yn(x))|x=0= =-2iW(U(x),V(x),y3(x),…yn(x))|x=0≠0, т.к W(0)=0,то W(U(x),V(x),y3(x),…yn(x))|x=0≠0 U(x),V(x),y3(x),…yn(x) –лин. незав. реш.(ФСР) 2)Кратные корни
λ1=λ2=…=λm=μ – корень кратности m характеристического уравнения системы (4) Теорема:
пусть
μ- корень кратности m
характеристического уравнения системы
(4), тогда система (5) имеет m
линейно независимых решений вида:
y=(γ0+γ1t+…+γm-1tm-1)eμx,
где γ0,γ1,γm-1
|
|
37.
Исследование
устойчивости положения покоя системы
двух ЛДУ с постоянными коэффициентами
в случае
Точки покоя:
det(A-λE) = 0
1)
Решение
периодично T= x(t)=x(t+T) y(t)=y(t+T) Все фазовые траектории замкнуты Центр
(нет асимптотической устойчивости) |
38.
Исследование устойчивости положения
покоя системы двух ЛДУ с постоянными
коэффициентами в случае
Точки покоя:
det(A-λE) = 0
1)
Матрица А имеет 1 линейно независимый
собственный вектор (к
а)
асимптоти-чески устойчивая система
Устойчивый вырожденный узел |
39.
Исследование устойчивости положения
покоя системы двух ЛДУ с постоянными
коэффициентами в случае
Точки покоя:
det(A-λE) = 0
Точек покоя бесконечное множество
Все
точки покоя заполняют прямую
а)
|
|
40. Нелинейные системы. Исследование устойчивости по первому приближению. Теорема Ляпунова. dx/dt=f(t,x);(9)
dxi/dt=fi(t,x1…xn);
f(t, пусть система (9) предст. в виде dx/dt=A(t)x+R(t,x) (10) где
А(t)=aij(t),
где aij(t)
Тогда dx/dt=A(t)x называется системой первого приближения для (9),(10). Теорема
Ляпунова:
пусть вектор-функция R(t,x)
непрерывно диффер. при
а
А(t) имеют отриц. действит. корни, то нулевое решение системы (9) и (10) асимптот. устойчивое. 2)если сущ. Корень характер. уравнения, имеющий положит.действит. числа, то нулевое решение системы неустойчиво. (БЕЗ ДОКАЗАТЕЛЬСТВА) Теорема. Если вектор-функция f(x) дважды непрерывно диффер. В окрестности точки х=0 и f(0)=0, то система dx/dt=f(x) приводится к виду dx/dt=A(t)x+R(t,x) и для нее справедливы условия теоремы Ляпунова. |
35. Понятие фазового пространства и фазовой траектории. Автономные системы ОДУ, св-ва их фазовых траекторий.
Считается,
что
Пусть
Кривая
Г: -интегральная кривая системы (6) Гс Определение.
Пространство
Определение.
Если
функции
То система ОДУ называется автономной Определение.
Точка
|
34. Теорема об устойчивости системы ЛДУ с постоянными коэффицентами. (5)
Все решения системы определены на всей числовой оси Рассмотрим
характеристическое уравнение системы:
det(A-λE)=0;
Теорема
3. 1) если все корни характеристического
уравнения системы (5)
Имеют отрицательные действительные части (т.е.
Замечание.
1)
Если
2)Если
|
|
|
36.
Исследование
устойчивости положения покоя системы
двух ЛДУ с постоянными коэффициентами
в случае
Находим точки покоя
(x0,y0)
— точка прямой
1°
|
|
|
39. асимптотической устойчивости нет так как:
б)
2)
Решение
ненулевое неограниченно
II)
A
|
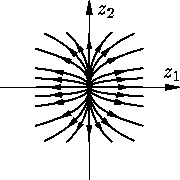
б)
Неустойчивый вырожденный узел
2)
Матрица А имеет 2 линейно независимых
собственных вектора
a) асимптотически устойчивая система устойчивый дикритический узел
б) неустойчивый дикритический узел
|
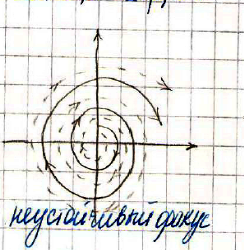
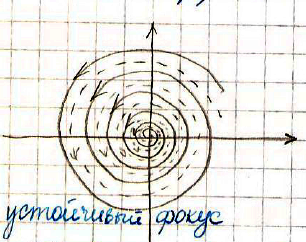
37.
Система асимптотически устойчива; фазовые траектории: спирали, накрученные на точку покоя
Устойчивый фокус
а)
Система
неустойчива; фазовые траектории:
раскрученные спирали
Неустойчивый фокус
|
|
|
Свойства фазовых траекторий автономной системы 1)
Если
точка
Док-во:
2)
Если
Док-во:
Замечание:
Точка покоя
3)
Если фазовая траектория отлична от
точки покоя, то она является гладкой
кривой(т.е. в каждой её точке
4)
Если
5)
6)
|
|
|
|
|
|

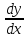 =Ay
необходимо и достаточно, чтобы λ было
собственным значением матрицы А, а γ
собственным вектором, соответствующим
собственному значению._)
следует,
что
а y1(x)..
yn(x)
–
решениея сист. (3). Докажем лин незав
y1(x)..
yn(x):
Вычислим опр. Вронского этих функ. в
x0=0:
W(0)=[y1e1x…ynenx]=
W(γ1*e1x…
γn*enx)≠0,
т.к. соб.век. γ1…γn,
матр.А, относящ. К различ. соб.знач. 1…
n
– лин.незав. Т.к. W(0)≠0,
то y1(x)..
yn(x)-лин.незав.След.,
они образуют ФСР. Общ. реш. имеет вид:
C1γ1e1x+…+
Cnγnenx
,
где
C1...Cn
– произв числа (копл).
=Ay
необходимо и достаточно, чтобы λ было
собственным значением матрицы А, а γ
собственным вектором, соответствующим
собственному значению._)
следует,
что
а y1(x)..
yn(x)
–
решениея сист. (3). Докажем лин незав
y1(x)..
yn(x):
Вычислим опр. Вронского этих функ. в
x0=0:
W(0)=[y1e1x…ynenx]=
W(γ1*e1x…
γn*enx)≠0,
т.к. соб.век. γ1…γn,
матр.А, относящ. К различ. соб.знач. 1…
n
– лин.незав. Т.к. W(0)≠0,
то y1(x)..
yn(x)-лин.незав.След.,
они образуют ФСР. Общ. реш. имеет вид:
C1γ1e1x+…+
Cnγnenx
,
где
C1...Cn
– произв числа (копл). R,
=
+ i-корни
хар-го урав-ия, -соб.знач.,
γ≠0-
соб.век.
y=γ*ex
по теор (11) реш. сист-мы (3).
R,
=
+ i-корни
хар-го урав-ия, -соб.знач.,
γ≠0-
соб.век.
y=γ*ex
по теор (11) реш. сист-мы (3).
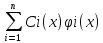
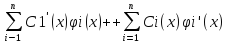 ;
;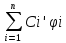 +
+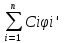 =A(x)
=A(x)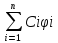 +
+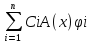 +b(x)
+b(x)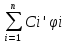 +
+
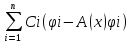 =b(x)
=b(x)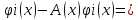
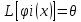
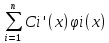 =b(x)
=b(x)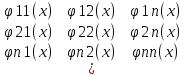 )
-
фундаментальная
матрица
)
-
фундаментальная
матрица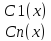 ) , Ф(x)C’(x)=b(x)
) , Ф(x)C’(x)=b(x) ]
]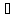 x
x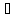 I
: det Ф(x)
I
: det Ф(x)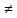 0
, значит
0
, значит
 Ф-1(x)
Ф-1(x)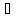 C(I)
C(I)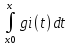
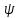 (x)=
(x)=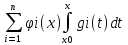

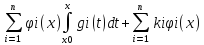
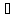 хотя бы одно (асимтотически) устойчивое
решение.
хотя бы одно (асимтотически) устойчивое
решение.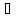 хотя
бы одно (асимтотически) устойчивое
решение. В противном случае система
ЛДУ является неустойчивой.
хотя
бы одно (асимтотически) устойчивое
решение. В противном случае система
ЛДУ является неустойчивой.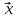 =
=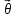 -
устойчиво, если
-
устойчиво, если
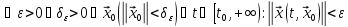
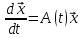
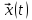 назывется ограниченной на множестве
назывется ограниченной на множестве
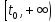 ,
если
,
если
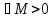 такое, что
такое, что

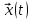 =
=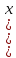
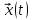 является
ограниченной на
является
ограниченной на
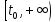 в том и только в том случае, когда
в том и только в том случае, когда
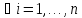 ограниченна на
ограниченна на
 функция
функция
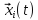
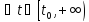 ||
||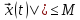 ,
то
,
то
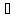 i=1,…,n
i=1,…,n
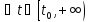 :
|x(t)|
:
|x(t)|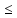 ||
||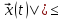 M
M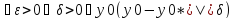
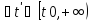
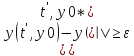 (t-время)
(t-время)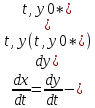
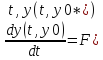
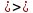
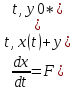
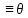
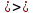 y(t)=y(t,y0*),
y(t)=y(t,y0*),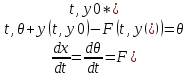
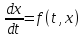
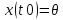
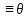 задачи
(1’),(2’)
задачи
(1’),(2’)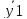 (x),
y3(x),…,
yn(x)
- ФСР системы(5) и y1(x)=U(x)+iV(x),
а
(x),
y3(x),…,
yn(x)
- ФСР системы(5) и y1(x)=U(x)+iV(x),
а
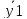 =U(x)-iV(x)
, где U(x),
V(x)
– действительные вектор-функции, то
U(x),
V(x),
y3(x),…,
yn(x)
образуют ФСР системы.
=U(x)-iV(x)
, где U(x),
V(x)
– действительные вектор-функции, то
U(x),
V(x),
y3(x),…,
yn(x)
образуют ФСР системы.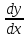 =Ay
(3) A=||aij||n×n
aij
=Ay
(3) A=||aij||n×n
aij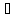 C,
пусть
C,
пусть
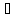 Cn
Cn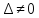 ,
,
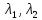 -
комплексные.
-
комплексные.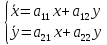 A=
A= ,
,
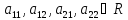 ;
;
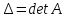
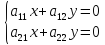
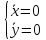 ,
,
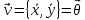
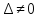 ,
единственная точка покоя (0,0).
,
единственная точка покоя (0,0).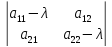 =0
– характеристическое уравнение.
=0
– характеристическое уравнение.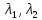 – корни
характеристического уравнения.
– корни
характеристического уравнения.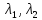
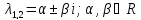
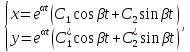
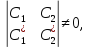
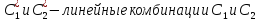
 =0,
=0,
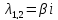 ,
,
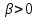 ,
,
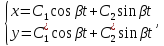
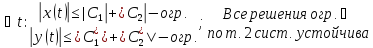
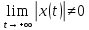 ,
т.е. нулевое реш. не явл. асимптотически
уст.
,
т.е. нулевое реш. не явл. асимптотически
уст.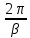

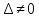 ,
,
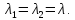
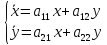 A=
A= ,
,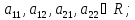
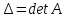
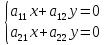
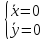 ,
,
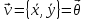
 ,
единственная точка покоя (0,0).
,
единственная точка покоя (0,0).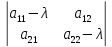 =0
– характеристическое уравнение.
=0
– характеристическое уравнение.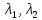 – корни
характеристического уравнения.
– корни
характеристического уравнения. кратные
корни
кратные
корни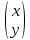 =
=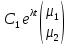 +
+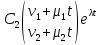
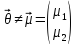 -собственный
вектор, отвечающий
-собственный
вектор, отвечающий
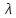
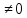 )
)
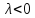
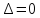 .
.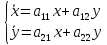 A=
A= ,
,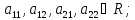
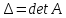
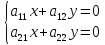
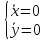 ,
,
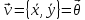
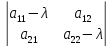 =0
– характеристическое уравнение.
=0
– характеристическое уравнение.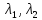 – корни
характеристического уравнения.
– корни
характеристического уравнения.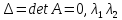 =0,
пусть
=0,
пусть
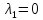 .
.
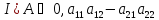 =0.
=0.
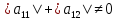
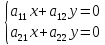

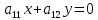
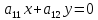
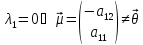 .
.
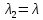 .
.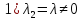 ,
, =
=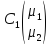 +
+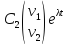 параметрическое
задание прямой с направляющим вектором
параметрическое
задание прямой с направляющим вектором
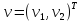
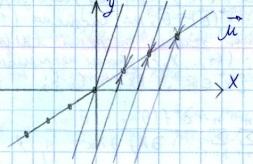
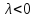 все решения ограничены система
устойчива.
все решения ограничены система
устойчива.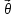 )=
)= ;
; [t0;
[t0;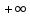 )
выполняется неравенство:
)
выполняется неравенство: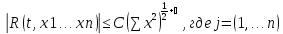
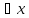 (IIxII<C0)
и для
(IIxII<C0)
и для
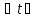 [t0;
[t0;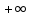 )
)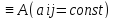 ,
тогда 1)если все корни det(A-λE)
= 0
,
тогда 1)если все корни det(A-λE)
= 0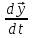 =
=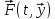 (6)
(6)
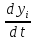 =
=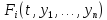 i=1,…,n
i=1,…,n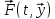 определена и непрерывно дифференцируема
в области G
определена и непрерывно дифференцируема
в области G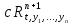
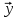 =
=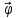 (t),
t
(t),
t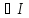 –решение системы (6)
–решение системы (6)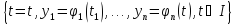 –
–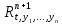 – пространство решений
– пространство решений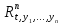 называется фазовым пространством
системы (6), а кривая
называется фазовым пространством
системы (6), а кривая
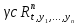 ,
задаваемая направлением
,
задаваемая направлением
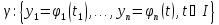 ,
где
,
где
 =
=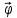 (t)=(
(t)=( -
решение системы (5), называется фазовой
траекторией системы (5).
-
решение системы (5), называется фазовой
траекторией системы (5).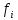 не зависят явно от
не зависят явно от
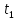 ,
т.е. система имеет вид (7)
,
т.е. система имеет вид (7)
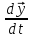 =
=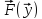 ;
;
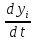 =
=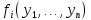
 =(
=(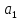 ,…,
,…,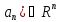 называется точкой покоя (положением
равновесия) автономной системы (7),
если
называется точкой покоя (положением
равновесия) автономной системы (7),
если
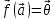 ,
т.е.
,
т.е.
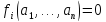
 =
=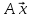 A=||
A=||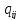 |
| ;
;
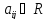
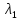 ,
, -корни
характеристического уравнения.
-корни
характеристического уравнения.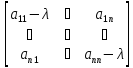 =0
=0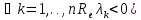 ,
то система асимптотически устойчива.
2) если
,
то система асимптотически устойчива.
2) если
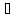 хотя бы 1 корень характеристического
уравнения с положительной действительной
частью (т.е.
хотя бы 1 корень характеристического
уравнения с положительной действительной
частью (т.е.
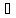 к:
к:
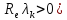 ,
то система (5) неусточива
,
то система (5) неусточива <0,
n
<0,
n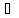 N,
N,
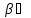 R,
то функции:
R,
то функции:
 ,
,
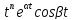 ,
,
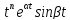 ограничены на [0,+
ограничены на [0,+ и
и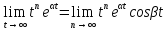 =
=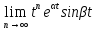 =0;
=0;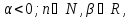 то
то
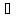 многочлена
многочлена
 степени n
функции:
степени n
функции: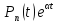 ,
,
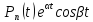 ,
,
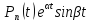 -
ограниченны на [0,+
-
ограниченны на [0,+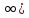
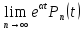 =0;
3) Если
=0;
3) Если
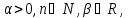 то функции
то функции
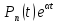 ,
,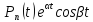 ,
,
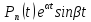 и
и
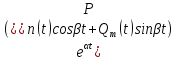 -
неограниченны на [0,+
-
неограниченны на [0,+
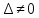 ,
,
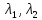 -
действительные.
-
действительные.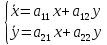
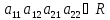
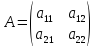 ,
,
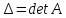

 — вектор скорости
— вектор скорости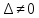 — единственная
точка покоя (0,0)
— единственная
точка покоя (0,0)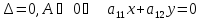
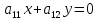
 — все точки
плоскости есть точки покоя.
— все точки
плоскости есть точки покоя.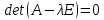
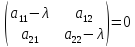 —
характеристическое
уравнение
—
характеристическое
уравнение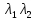 —
корни
—
корни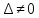 ,
,
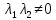
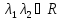 ,
,
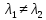
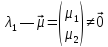
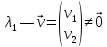
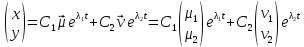 — общее решение
— общее решение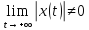
 неустойчивая система
неустойчивая система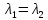 =0
=0 =
=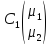 +
+ ,
,
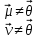
 система неустойчива.
система неустойчива.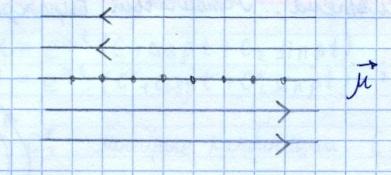
 точки покоя - все точки плоскости
точки покоя - все точки плоскости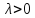 неустойчивая система
неустойчивая система
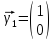 ,
,
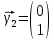
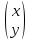 =
=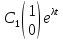 +
+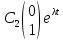 =
=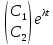
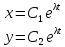 ,
,
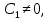 y=
y=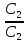 x
x


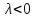 ,
,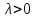 неустойчивая система
неустойчивая система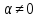 а)
а)
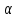 =Re
=Re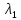 ,
,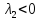 ,
,
 =Re
=Re ,
,
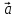 =(
=( ,…,
,…,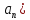 -точка
покоя системы (7), то вектор-функция
-точка
покоя системы (7), то вектор-функция
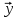 (t)
(t)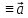 является решением системы (7)
является решением системы (7)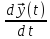 =
=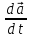 =
=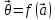 =f(
=f(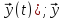 (t)
(t)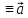 -
решение (7)
-
решение (7)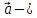 точка
покоя системы (7), то
точка
покоя системы (7), то
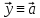 – фазовая траектория системы (7)
– фазовая траектория системы (7)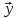 (t)
(t)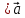 -
решение (7)
-
решение (7)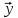 =
=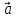 называется (ассимтотически) устойчивой
или неустойчивой, если устойчиво или
(ассимтотически устойчиво или
неустойчиво) решение
называется (ассимтотически) устойчивой
или неустойчивой, если устойчиво или
(ассимтотически устойчиво или
неустойчиво) решение
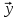 (t)
(t)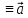 .
.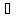 ненулевой
касательный вектор).
ненулевой
касательный вектор).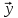 =
=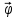 (t)-
решение системы (7), то для
(t)-
решение системы (7), то для
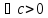 вектор-функция
вектор-функция
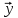 =
=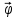 (t+с)-
также решение системы (7) и фазовые
траетории этих решений совпадают.
(t+с)-
также решение системы (7) и фазовые
траетории этих решений совпадают.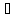 2 фазовые траектории либо не пересекаются,
либо совпадают.
2 фазовые траектории либо не пересекаются,
либо совпадают. следующие типы фазовых траекторий:
1. Точка (положение равновесия); 2.гладкая
замкнутая кривая (цикл); 3.гладкая
кривая без точек самопересечения;
следующие типы фазовых траекторий:
1. Точка (положение равновесия); 2.гладкая
замкнутая кривая (цикл); 3.гладкая
кривая без точек самопересечения;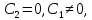
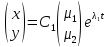 —2 луча,
соответствующих
—2 луча,
соответствующих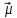 .
.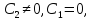
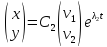 —2 луча,
соответствующих
—2 луча,
соответствующих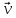 .
.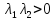 ,
,
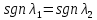
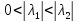
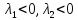 — система
асимптотически устойчива.
— система
асимптотически устойчива.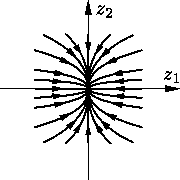
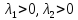 (
(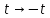 )
)
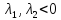 ,
,
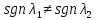

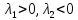 — система
неустойчива.
— система
неустойчива.