Билет № 23

1. Через заданную точку М₀ провести прямую L параллельно заданной прямой L₀.

2. Задание прямой L точкой М₀єL и направляющим вектором этой прямой.

3. Отклонение д(М₀,L) точки М от прямой L.

4. Характеристическое свойство гиперболы. Эксцентриситет.

5. Через точку М₀ (не лежащую на параболе) провести касательную прямую. Рисунок.

6. Первая теорема Аполлония для эллипса.

7. Отрезок ав является общим перпендикуляром прямых l1 и l2. Точка АєL1; Точка ВєL2. Найти координаты точек а, в.

L₁:

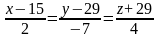
L₂:

8. Вычислить расстояние между двумя прямыми:

L₁:

L₂:

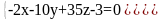
9. Найти уравнение общего перпендикуляра пары прямых l1 и l2, где

L₁:

L₂:

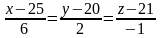
10. Через точку А(-11,0) провести прямую перпендикулярно заданной прямой : .Рисунок.

11. Найти координаты основания перпендикуляра АН, опущенного из точки А(3,-9,6) на плоскости

: 2х+18у-17z-359=0 и : 3х+2у+z-11=0.

12. Через точку А(-8,10) провести прямую параллельно заданной прямой : 8x-y-1=0 .Рисунок.

13. Найти точку пересечения плоскости П: 9х+4у-211=0 с прямой .

14. Из точки P(-16;9) проведены касательные к эллипсу . Вычислить расстояние d от точки Р до хорды эллипса, соединяющей точки касания.

15. Гипербола проходит через точку А( ;3) и касается прямой 9х+2у-15=0 . Составить уравнение этой гиперболы при условии, что ее оси совпадают с осями координат.

16. Определить, как расположена прямая х-у-3=0 относительно гиперболы 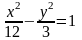: пересекает ли, касается или проходит вне ее.

«Оформили: Белов Илья, Джепарова Фериде ст. 201-П, 2011»

Контрольная работа по аналитической геометрии для студентов I курса

Лектор В. И.Мягков

Билет № 24

1. Теорема о задании плоскости в пространстве общим уравнением Ax+By+Cz+D=0. Вектор нормали.

2. Через заданную точку М₀ провести прямую L параллельно заданной прямой L₀.

3. Угол между двумя прямыми на плоскости. Рисунок.

4. Асимптота гиперболы не имеет ни одной общей точки с гиперболой. Доказать.

5. Каноническое уравнение эллипса. Соотношение между a, b и c.

6. Диаметр параболы, сопряженный вектору неасимптотического направления. Рисунок.

7. Отрезок АВ является общим перпендикуляром прямых L₁ и L₂. Точка АєL₁; Точка ВєL₂. Найти координаты точек А, В.

L₁:

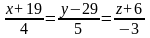
L₂:

8. Вычислить расстояние между двумя прямыми:

L₁:

L₂:

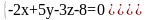
9. Найти уравнение общего перпендикуляра пары прямых L₁ и L₂, где

L₁:

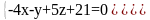
L₂:

10. Через точку А(-1,3) провести прямую перпендикулярно заданной прямой : 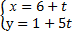.Рисунок.

11. Найти координаты основания перпендикуляра АН, опущенного из точки А(-5,1,2) на плоскости

: 16х+2у+5z-217=0 и : -х+5у+9z-135=0.

12. Через точку А(-1,3) провести прямую параллельно заданной прямой : 4x+y+2=0 .Рисунок.

13. Найти точку пересечения плоскости П: 8х-у+7z+235=0 с прямой .

14. Из точки С(1;-10) проведены касательные к гиперболе . Составить уравнение хорды, соединяющей точки касания.

15. Составить уравнение гиперболы, касающейся прямых 5х-6у-16=0, 13х-10у-48=0, при условии, что ее оси совпадают с осями координат.

16. Дан эллипс . Его диаметр |PP1|=12. Найти длину диаметра, сопряжённого данному.

«Оформили: Белов Илья, Джепарова Фериде ст. 201-П, 2011»

Контрольная работа по аналитической геометрии для студентов I курса

Лектор В. И.Мягков