Билет № 19

1. Переход от общего уравнения плоскости к её нормированному уравнению.

2. Через заданную точку М₀ провести прямую L параллельно заданной прямой L₀.

3. Расстояние между двумя прямыми в пространстве.

4. Пара взаимно сопряженных диаметров гипербол. Начертить.

5. Касательная к эллипсу, проходящая через точку М_0, лежащую на эллипсе.

6. Через точку М₀ (не лежащую на параболе) провести касательную прямую. Рисунок.

7. Отрезок АВ является общим перпендикуляром прямых L₁ и L₂. Точка АєL₁; Точка ВєL₂. Найти координаты точек А, В.

L₁:

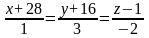
L₂:

8. Вычислить расстояние между двумя прямыми:

L₁:

L₂:

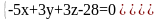
9. Найти уравнение общего перпендикуляра пары прямых L₁ и L₂, где

L₁:

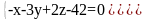
L₂:

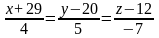
10. Через точку А(3,9) провести прямую перпендикулярно заданной прямой : 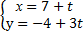.Рисунок.

11. Найти координаты основания перпендикуляра АН, опущенного из точки А(-1,3,0) на плоскости

: 7х+2у+7z-101=0 и : 8х+5у+2z-100=0.

12. Через точку А(-11,0) провести прямую параллельно заданной прямой : 3x-2y-9=0 .Рисунок.

13. Найти точку пересечения плоскости П: 14х+3у+371=0 с прямой .

14. На параболе найти точку М, ближайшую к прямой 4х+3у-14=0, и вычислить расстояние d от точки М до этой прямой.

15. Дана парабола .Составить уравнение хорды, которая точкой P(2;5) делится пополам.

16. Большая ось гиперболы равна 16 и эксцентриситет = 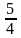. Составить уравнение гиперболы.

Контрольная работа по аналитической геометрии для студентов I курса

«Оформили: Белов Илья, Джепарова Фериде ст. 201-П, 2011»

Лектор В. И.Мягков

Билет № 20

1. Переход от общего уравнения плоскости к её нормированному уравнению.

2. Расстояние между парой параллельных прямых на плоскости. Рисунок.

3. Отклонение точки от прямой на плоскости.

4. Угловые коэффициенты К₁ и К₂ пары взаимно сопряженных диаметров эллипса.

5. Число точек пересечения прямой с параболой. Возможные случаи. Рисунок.

6. Первая теорема Аполлония для гиперболы.

7. Отрезок АВ является общим перпендикуляром прямых L₁ и L₂. Точка АєL₁; Точка ВєL₂. Найти координаты точек А, В.

L₁:

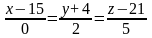
L₂:

8. Вычислить расстояние между двумя прямыми:

L₁:

L₂:

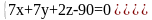
9. Найти уравнение общего перпендикуляра пары прямых L₁ и L₂, где

L₁:

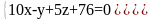
L₂:

10.

Через точку А(0,-6) провести прямую перпендикулярно заданной прямой : .Рисунок.

11. Найти координаты основания перпендикуляра АН, опущенного из точки А(5,0,6) на плоскости

: 4х+12у-7z-187=0 и : 7х-4у+z-107=0.

12. Через точку А(1,6) провести прямую параллельно заданной прямой : x-y+3=0 .Рисунок.

13. Найти точку пересечения плоскости П: 3х+9у-4z+61=0 с прямой .

14. Найти геометрическое место точек, из которых можно провести перпендикулярные касательные к параболе .

15. Составить уравнение диаметра параболы , проходящего через середину её хорды, отсекаемой на прямой .

16. Найти точки пересечения прямой 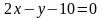и гиперболы .

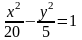Контрольная работа по аналитической геометрии для студентов I курса

Лектор В. И.Мягков