2.1 Статистическое моделирование.
Статист. Моделир-е – способ исслед-я процессов поведения вероятностных систем в условиях , когда неизвестно внутр взаимодействие в этих с-мах. Она заключается в м ашинной имитации изучаемого процесса объекта со всеми сопровождающими его случайностями, при этом исп-ся методы мат. Статистики и теории вероятностей.
2.2. Метод Монте-Карло.
Для стат модел-я ( модел-е случайных величин) как численный м-д решения мат задач исп-ся м-д Монте-Карло, кот был разработан в 1949 г. амер ученым Дж. Нейманом и С.Уланом. в СССр перв раб в 1955-1956гг, когда появился перв ЭВМ.
Смысл м-да МК состоит в том, что исслед. Процесс моделир-ся путем многократных повторений его случайных реализаций. Единичные реал-ии наз-ся статистич-ми испытаниями. В м-де МК некот велич Х ставится в соответ-е некот случ велич КСИ- матем ожидание , среднее кот рав-ся Х.
Велич КСИ моделир-ся на ЭВм, и среднее по большому кол-ву испытаний принимаетсяся за приближенное Х.
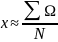N-
число испытаний, Ω-результаты i-го
испытания и реализ-ии.
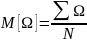-матем ожидание случ велич-ны,
характеризует среднее значение.
-
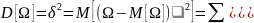дисперсия, харак-ет отклонение СВ от
сред значения или меру разброса сред
значения.
СВ полностью опред-ся заданием плотности вероятностей ( ф-я распред-я СВ)
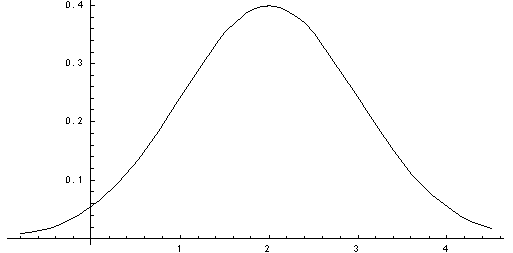
Нормальный
закон распределения:
Для норм СВ справедливо правило 3х сигм:
Р(х)
х
мх
Используя
прав 3 сигм и центр теорему ( сумма
большого числа одинак СВ приблизит-но
подчиняется ном з-ну):
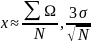
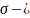сред квадрат отклонение.
2.3 Стохастическое моделир-е. Элементы теории марковских процессов.
Стох модел-е отражает вероят-ти процесса и события объекта , имеет дело со стохаст моделями. Стохаст м-ли- более общее понятие, чем статистическое.
Стохаст м-ль – м-ль, в кот параметры, условия, ф-я и харак-ки состояния моделир-гот объекта представлены СВ и связаны стохаст зависимостями, либо исход инфо в них представл СВ. при построении стох м-лей прим-ся м-ды корреляц и регрессион анализа и др статист м-ды и теория случайных процессов, в частности теор марковских процессов (ТМП), кот заним-ют особое место среди случ процессов.
Стационарные
случ процессы- поток событий, вероятность
появления событияна участке (t,
t+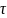
)
зависит лишь от длины участка
И не зависит от t;
в противном случае - нестационар
процессы.
2 основных св-ва марковских проц-ов:
Ординарность;
Отсутствие последействия.
Поток
событий наз-ся ординарным, ЕС вероят-ти
осуществления на бесконечно малом
участке времени
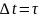
2,3 и более событий пренебрежимо малы по сравнению с вероят-тью 1го события ( это поток относительно редких событий)
(
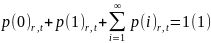
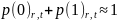в силу свойств ординарности)
-
на интер (t,
t+
)
произойдет I
шт событий. если =0, то ни одно событие
не произойдет.
Отсутствие
последовательности обозначает, что
для любых перекрещивающихся участков
длиной
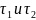число событий, случившихся на на одном
из них, не зависит от того, сколько
событий произошло на др.
Для Марковских процессов будущее состояние в с-ме не зависит токо от известного наст состояния (процессы без памяти).
Название Марков процесса дано в честь рус матем-ка А.А Маркова( 1856-1929)
Выделяют 3 основных типа МП:
Марковские цепи;
Марков разрывные процессы ( дискретные в пространстве и во времени);
Непрерывные марк пр-цы.
Модель рождения и гибели связ с решением зад, связан-х с оценкой численности популяции и анализом распростр-я эпидемии.
Пусть х(t)- СВ, как положит, так и отрицательные скачки имеются.
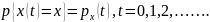
Пусть
в момент времени t
с-ма находится в состоянии х. вероятность
того, что (t,
t+
)
перейдет из состояния х в состояния:
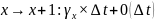
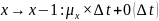
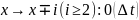
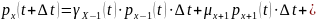
переносим
в левую часть, обе части дифференцируем
и переходим к логарифму:
-
система
разрывных сил.
---
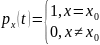начальное условие
В природе нет Марковских процессов, они нужны для описания систем массового обслуживания.