6.6 Интерполяция кривых методом в-сплайнов

Задачей интерполяции кривых методом Безье и методом В-сплайнов является нахождение характеристической ломаной, которая однозначно определяет заданную кривую, причем должны выполняться все интерполяционные ограничения.

В случае построения кривых методом В-сплайнов необходимо иметь зависимость между опорными точками кривой S_i и точками характеристической ломаной P_i и узлами u_i. Через p_i : = u обозначим значение параметра из интервала (u₀, u_n), которое оказывает максимальное влияние на форму кривой, а через S_i – соответствующую точку кривой. Тогда имеет место зависимость.

S_i = Q (p_i).

Если известны значения параметров p_i, то для опорных точек кривой S_i можно составить следующую систему уравнений:

.

B мaтpичнoй фopмe этy cиcтeмy мoжнo пepeпиcaть cлeдyющим oбpaзoм:

(S_i) = (Q(p_i)) = (U^T(p_i))P_i

или

S = U^TP.

Отсюда можно получить решение этой системы в виде:

P = (U^T)^-1S,

т. е. найдена искомая зависимость:

P_i = .

Для интерполяции кривой методом В-сплайнов надо установить соответствие между точками кривой P_i и значениями параметров p_i, от которых зависит форма кривой. Эти значения параметров определяют «качество» интерполяционной кривой. O «кaчecтвe» интepпoляциoннoй кpивoй мoжнo cyдить, например, пo oтклoнeнию oт aнaлитичecки зaдaннoй кpивoй, нaличию ocцилляций или пoявлeнию пeтeль.

6.7 Конструирование поверхности по Фергюсону

Для решения задач, связанных с приближением функций и описанием поверхностей, широко применяются параметрические сплайны (например, математический аппарат Фергюссона), среди которых в технических приложениях наибольшее распространение получили сплайны нечетных степеней. Частным случаем параметрического сплайна является сплайн с векторными коэффициентами бикубической степени. Элемент разбиения с вершинами в точках Р(0,0), Р(1,0), Р(0,1) и Р(1,1) задается изопараметрическими кривыми P(u,0), P(u,l), P(0,v) и P(l,v), соединяющими эти вершины (рисунок 6.20). Кривая в форме Фергюсона определяется координатами концевых точек и значениями производных в них. Если такие четыре кривые замкнуть, то полученный контур можно рассматривать как границу отсека (участка). Параметры выбираются в соответствии c рисунком 6.20.

Внyтpeнняя чacть пoвepxнocти тaкжe oпpeдeляeтcя c пoмoщью кpивыx в фopмe Фepгюcoнa, кoтopыe в зaвиcимocти oт пapaмeтpoв u и v coeдиняют двe пpoтивoлeжaщиe гpaницы oтceкa. Тaк кaк гpaницы oтceкa yжe caми зaдaют кoнцeвыe тoчки пepeмeннoй кpивoй, тo для иx oпpeдeлeния нe тpeбyeтcя зaдaния пapaмeтpичecкиx пpoизвoдныx. Kpивыe AD и BC oпpeдeляют кoнцeвыe тoчки кpивoй RT, кoтopaя измeняeтcя в v-нaпpaвлeнии. Пapaмeтpичecкиe производныe переменной кpивoй для пapaмeтpa v = 0 и v = 1 должна быть идeнтичны пapaмeтpичecким пpoизвoдным гpaниц oтceкa дA/дu, дB/дu, дC/дu, дDlдu. Чтoбы oпpeдeлить пpoизвoдныe для дpyгиx знaчeний пapaмeтpa v, в тoчкax E, F, G и H фикcиpyют пpoизвoльныe вeктopы дE/дv, дF/дv, дG/дv и дH/дv.

Этим определены кривые EH и FG , а следовательно, и параметрические производные:

и .

Кривые, изменяющиеся в зависимости от параметра u, получаются аналогично, если в точке I определить векто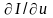р и проделать аналогичные действия для остальных вершин. Но теперь векторы выбираются не произвольным образом, а в зависимости от уже выбранных векторов, например:

.

Каждая кривая одного семейства пересекается со всеми кривыми другого семейства.

Рисунок 6.20 – Параметрически заданный участок поверхности

Участок поверхности по Фергюссону задается формулой:

где r_u, r_v - касательные векторы, выставленные в узловых точках участка к граничным и- и v-кривым;

r_uv - векторы "закрутки".

При этом удобно перейти от параметров t и s к параметрам U и V, используя формулы:

Функции при этом определяются при подстановке в них значений параметров U и V.

Векторы закрутки, кратные перекрестной производной функции, обеспечивают гладкость поверхности в месте схождения четырех углов.

Математический аппарат, предложенный Фергюссоном, осуществляет построение интерполяционной поверхности через узловые точки, обеспечивает требуемый порядок гладкости, легко реализуется на практике. Задание поверхности касательными векторами увязывается со способом получения эквидистантных кривых, что может быть использовано для определения траектории движения фрезы при обработке поверхности на станках с ЧПУ.