Раздел 3: Аналитическая геометрия Уравнение прямой

Пусть на плоскости задана прямоугольная система координат. Составим уравнение прямой , проходящей через две заданные различные точки и . Пусть есть произвольная точка. Рассмотрим векторы и . Легко видеть, что тогда и только тогда, когда , то есть, согласно теоремы 1 пункта 2 § 1, , где . Приравняв координаты, получим соотношения , . Из этих соотношений выведем уравнение прямой :

. (1)

Уравнение (1) называется уравнением прямой, проходящей через заданные точки и . Равенство (1) можно преобразовывать к следующему виду:

, (2)

в котором , , .

Соотношение (2) называется общим уравнением прямой. Если , то из (2) можно выразить : , где , . Число называется угловым коэффициентом прямой и , где угол между положительным направлением оси и данной прямой. Из (1) можно вывести также следующее соотношение

.

Данное равенство называется уравнением прямой, проходящей через точку и имеющей заданный угловой коэффициент .

Если прямая проходит через точки и , лежащих на осях и , то из (1) выведем соотношение , которое называется уравнением прямой в отрезках.

Геометрический смысл коэффициентов уравнения прямой

Теорема 1. Если (2) есть уравнение прямой , то .

Доказательство.

Возьмет две различные точки , . Тогда и , . Вычтем из второго равенства первое:

. Теорема доказана.

Любой вектор, перпендикулярный к прямой , называется вектором нормали к . Из (1) можно вывести еще одно соотношение:

,

которое называется уравнением прямой, проходящей через точку перпендикулярно вектору .

Обозначим , , . Любой вектор, параллельный прямой или принадлежащий прямой, называется направляющим вектором прямой. Используя данные обозначения, перепишем уравнение (1):

,

которое называется уравнением прямой, проходящей через точку параллельно вектору .

Задача 1. Доказать, что вектор является направляющим вектором прямой, заданной уравнением (2).

Задача 2. Доказать, что если прямая задана уравнением (2) и , то проходит через начало координат, если , то , если , то .

Расположение прямых на плоскости

Теорема 2. Пусть прямые , заданы уравнениями и и пусть есть угол между и . Тогда

. (3)

Прямая || тогда и только тогда, когда . Прямая тогда и только тогда, когда .

Доказательство.

Из теоремы 1 следует , . Пусть есть угол между и . Легко видеть, что если , то , если есть тупой угол, то . В первом случае . Во втором случае . Отсюда следует (3). Далее || ; . Теорема доказана.

Теорема 3. Пусть прямая задана уравнением (2). Расстояние от точки до прямой равно .

Полярные координаты

При решении многих задач на плоскости вместо декартовых прямоугольных координат вводят другие координаты. Одной из таких систем является полярная система координат.

П усть на плоскости задана прямая с отмеченной точкой и выбранным направлением . Ось называется полярной осью. Положение любой точки плоскости однозначно определяется парой чисел и , где , а есть угол, на который нужно повернуть против часовой стрелки ось до совпадения с вектором . Числа , называют полярными координатами точки и пишут . Число называют полярным радиусом, а - полярным углом точки .

Пусть на плоскости имеется также декартова система координат . Тогда точка имеет еще декартовы координаты . Связь полярных и декартовых координат задается формулами:

, , , , . (4)

Задача. Доказать формулы (4).

Приведем примеры линий, уравнения которых записаны в полярных координатах:

- окружность ; - луч ; - прямая , - спираль Архимеда (см. рис.).
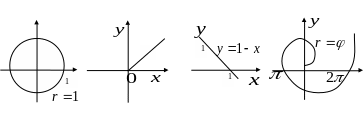