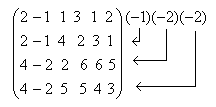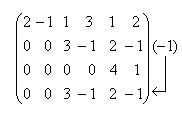Метод Крамера решения системы линейных уравнений

Пусть в системе (1) , то есть число уравнений равно числу неизвестных.

Обозначим определитель матрицы системы (1). Пусть есть определитель матрицы, полученной из матрицы заменой го столбца столбцом свободных членов .

Теорема (Крамера). Если в системе (1) и определитель то система (1) имеет единственное решение .

Пример. Решить систему:

(3)

Найдем , , ,

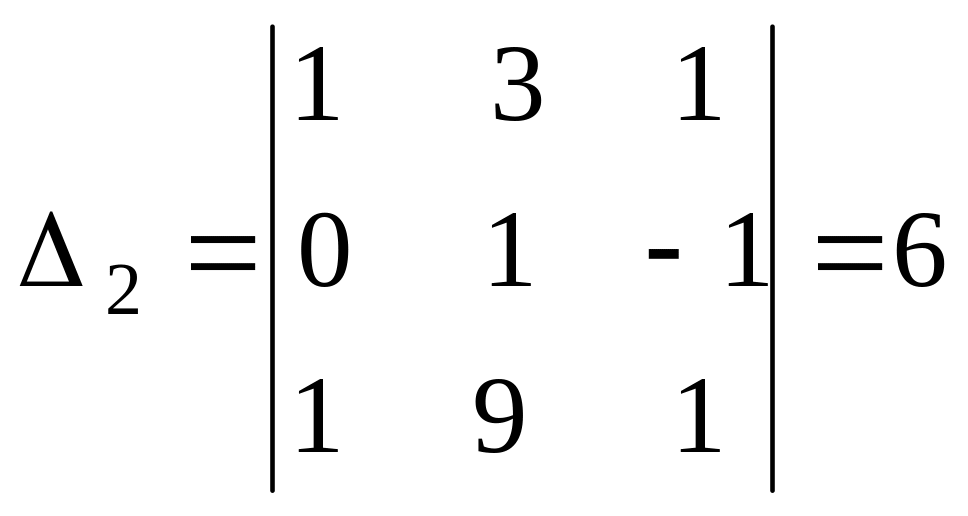Тогда , , .

Матричный метод

Пусть в системе (1) также .

Теорема. Если определитель матрицы системы (1) не равен 0, то есть , то система (1) имеет единственное решение . Здесь - матрицы столбцы неизвестных и свободных членов соответственно.

Доказательство. Так как , то существует обратная матрица . Умножим равенство (2) слева на матрицу : , , , . Теорема доказана.

Задача. Доказать что для любой матрицы порядка и единичных матриц порядков и соответственно имеют место равенства .

Пример. Решим систему (3) матричным методом. Для этой системы выпишем матрицы

, , .

По формуле найдем обратную матрицу .

Из теоремы следует . Следовательно .

Метод Гаусса решения произвольной системы

Матричным методом и методом Крамера можно решать только такие системы, в которых число уравнений равно числу неизвестных и определитель матрицы системы не равен 0. В этом пункте будет рассмотрен метод, с помощью которого решается произвольная система.

Суть метода Гаусса состоит в том, что с помощью специальных преобразований система (1) заменяется на равносильную систему, матрица которой является ступенчатой.

Определение. Матрица называется ступенчатой или треугольной, если ее нулевые строки лежат ниже всех ненулевых строк, и если первый не равный нулю элемент ее любой ненулевой строки, начиная со второй, расположен правее первого не равного нулю элемента предыдущей строки.

Пример. Ступенчатыми являются следующие матрицы

, , , .

Систему, матрица которой является ступенчатой, также будем называть ступенчатой или треугольной.

Систему уравнений (1) будем приводить к ступенчатому виду с помощью элементарных преобразований 1 и 2-го типа.

Определение. Элементарным преобразованием 1-го типа называется преобразование, состоящее в том, что в системе (1) меняются местами два уравнения. Элементарным преобразованием 2-го типа называется такое преобразование системы (1), при котором все уравнения системы (1), кроме некоторого -го уравнения , не меняются а вместо -го уравнения записывается уравнение , где , .

Заметим, что элементарное преобразование 2-го типа состоит в том, что к -му уравнению прибавляется -е уравнение, умноженное на число .

Теорема. Две системы линейных уравнений равносильны, если одна получается из другой путем применения конечной последовательности элементарных преобразований 1-го и 2-го типов.

Опишем метод Гаусса приведения системы (1) к ступенчатому виду

Пусть в системе (1) коэффициент при в первом уравнении . Если это не так, то этого можно добиться перестановкой уравнений, то есть с помощью элементарного преобразования 1-го типа. Для этого нужно выбрать в системе (1) уравнение в котором коэффициент при не равен 0 и поменять его местами с первым уравнением.

Прибавим ко второму уравнению первое, умноженное на , к третьему уравнению прибавим первое, умноженное на и так далее, к последнему уравнению прибавим первое, умноженное на . Легко видеть, что в результате этих элементарных преобразований 2-го типа во всех уравнениях, начиная со второго, коэффициенты при станут, равными нулю. Для упрощения записи будем обозначать коэффициенты и свободные члены, полученной системы (эквивалентной системе(1)) также , , как и системы (1).

Пусть есть наименьший номер такой, что в уравнении, начиная со 2-го, имеется ненулевой коэффициент при неизвестной . Также как и выше, путем перестановки уравнений можно добиться того, чтобы .

Прибавим к третьему уравнению второе, умноженное на и так далее. К последнему уравнению прибавим второе уравнение, умноженное на .

В результате данных элементарных преобразований 2-го типа во всех уравнениях начиная с 3-го коэффициенты при станут равными нулю и первые три уравнения системы примут ступенчатый вид.

Проделав аналогичные выкладки далее, всю систему приведем к ступенчатому виду. Коэффициенты полученной системы обозначим так же , как и у системы (1). Если в системе образовались строки или столбцы, состоящие из одних нулей, то мы их отбросим.

Далее возможны три случая.

Первый случай. Последнее уравнение системы имеет вид , где , . Данное равенство неверно. Поэтому система решений не имеет.

Второй случай. Число уравнений в полученной системе равно числу неизвестных. В этом случае матрица системы является квадратной, на главной диагонали которой стоят ненулевые элементы, а под главной диагональю стоят нули. Данная система легко решается, начиная с последнего уравнения. Очевидно, что полученное решение единственное.

Третий случай. Число уравнений в последней системе меньше числа неизвестных .

Пусть есть первый слева ненулевой коэффициент в -ой строке матрицы последней системы. Здесь .

Определение. Неизвестные называются базисными. Остальные неизвестные называются свободными.

В третьем случае ступенчатая система решается следующим образом. Перенесем, все свободные неизвестные с их коэффициентами в правые части уравнений системы.

Решим полученную систему относительно базисных неизвестных так же, как во втором случае. Таким образом, решения исходной системы получаются следующим образом. Свободные неизвестные принимают произвольные действительные значения независимо друг от друга, а базисные выражены через свободные.

Как видим, в третьем случае система (1) имеет бесконечное число решений. Нами доказана следующая теорема.

Теорема. Система уравнений (1) либо несовместна (случай 1), либо имеет единственное решение (случай 2), либо имеет бесконечное множество решений.

Пример 1. Решить систему:

Решение. В соответствии с методом Гаусса обнулим коэффициенты при во втором и третьем уравнениях. Для этого вычтем из второго уравнения первое, а к третьему уравнению прибавим первое, умноженное на число :

Обнулим коэффициент при в третьем уравнении. Для этого прибавим к третьему уравнению второе, умноженное на :

Данная система имеет ступенчатый вид и легко решается. Из последнего уравнения найдем и подставим его во второе уравнение: . Подставим , в первое уравнение . Ответ: .

Замечание. При решении конкретных систем часто удобно использовать элементарное преобразование 3-го типа, состоящее в умножении какого-нибудь уравнения на число . Очевидно, что после этого преобразования получается равносильная система.

Пример 2. Решить систему:

Решение. Поменяем местами первое и второе уравнения

Прибавим ко второму уравнению первое, умноженное на 2, а к третьему уравнению прибавим первое, умноженное на 3:

Данная система примет ступенчатый вид, если поменять местами второе и третье уравнения. Система несовместна, поскольку второе равенство неверно.

Ответ: решений нет.

Пример 3. Решить систему.

Решение. Для сокращения записи все преобразования метода Гаусса будем записывать в расширенной матрице. Составим расширенную матрицу систему и приведем ее к ступенчатому виду методом Гаусса:

Этой расширенной матрице соответствует система

Данная система соответствует третьему случаю, когда число уравнений меньше числа неизвестных. В соответствие с определением свободными будут являться неизвестные . Перенесем в первом и втором уравнениях свободные переменные в правую часть:

Выражая из этой системы последовательно получим ответ.

Ответ: .

Таким образом, система в примере 3 имеет бесконечное число решений, то есть эта система является неопределенной.