Раздел 1: Линейной алгебры Матрицы

Определение. Матрицей называется прямоугольная таблица чисел, которые называются элементами матрицы.

Если матрица имеет строк и столбцов, то будем говорить, что матрица имеет размеры .

Матрицы обозначают заглавными латинскими буквами . Элементы матрицы обозначаются соответствующими строчными буквами с двумя индексами, указывающие номер строки и номер столбца в которых находится элемент матрицы. Так элемент матрицы находится в -й строке и -ом столбце.

Таким образом, матрица размера имеет вид

.

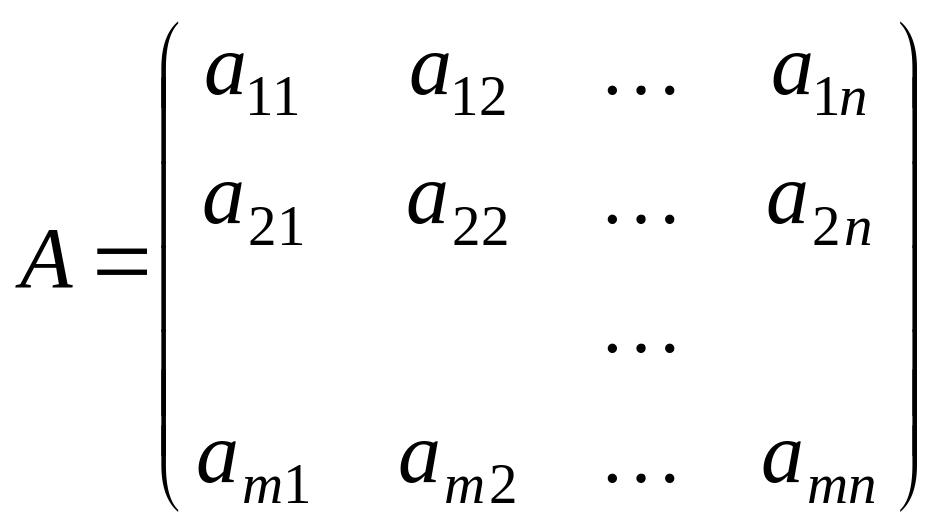Определение. Матрица называется квадратной, если число строк равно числу столбцов: . В этом случае число называют порядком квадратной матрицы.

Определение. Матрицы называются равными, если они имеют одинаковое количество строк и столбцов и на одинаковых местах стоят равные элементы.

Определение. Матрицей строкой называется матрица, имеющая одну строку. Матрицей столбцом называется матрица, имеющая один столбец. Матрица, все элементы которой равны нулю, называется нулевой.

Определение. Элементы квадратной матрицы, у которых номера строк и столбцов совпадают, называются диагональными элементами.

Для квадратной матрицы порядка диагональными элементами будут , ,…, .

Определение. Все диагональные элементы квадратной матрицы образуют главную диагональ матрицы. Диагональной называют такую квадратную матрицу, у которой вне главной диагонали стоят только нули. Единичной называется такая диагональная матрица, у которой все диагональные элементы равны 1. Единичную матрицу обозначают буквой .

Пример. 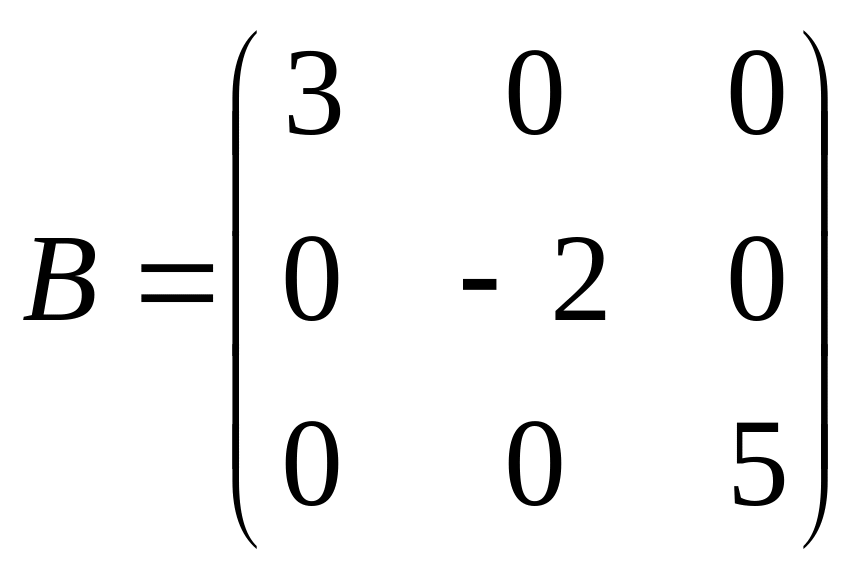- диагональная матрица 3-го порядка, - единичная матрица 2-го порядка.

Операции над матрицами

Произведение матрицы на число.

Определение. При произведении матрицы на число все элементы матрицы умножаются на данное число.

Сумма и разность матриц.

Складывать и вычитать можно только матрицы одинакового размера.

Определение. Суммой или разностью двух матриц одинакового размера называют третью матрицу, полученную путем сложения или вычитания соответствующих элементов данных матриц.

Произведение матриц.

Умножение двух матриц определено, если число столбцов первой матрицы равно числу строк второй матрицы.

Определение. Произведением матрицы размера на матрицу размера называется матрица размера такая, что каждый элемент матрицы равен сумме произведений элементов -ой строки матрицы на соответствующие элементы -го столбца матрицы :

=

Произведение матрицы на матрицу обозначается , то есть .

Пример. Пусть , . Тогда

.

Задача. Доказать что для любой матрицы порядка и единичных матриц порядков и соответственно имеют место равенства

.

Транспонирование матриц.

Матрица , которая получается из матрицы заменой в ней местами строк и столбцов называется транспонированной относительно матрицы .

Пример. Пусть . Тогда .

Определители

Каждой квадратной матрице порядка ставится в соответствие число , которое называется определителем матрицы порядка .

Определение. Определителем первого порядка квадратной матрицы первого порядка называется само число : . Определителем второго порядка матрицы называется число . Определителем третьего порядка матрицы =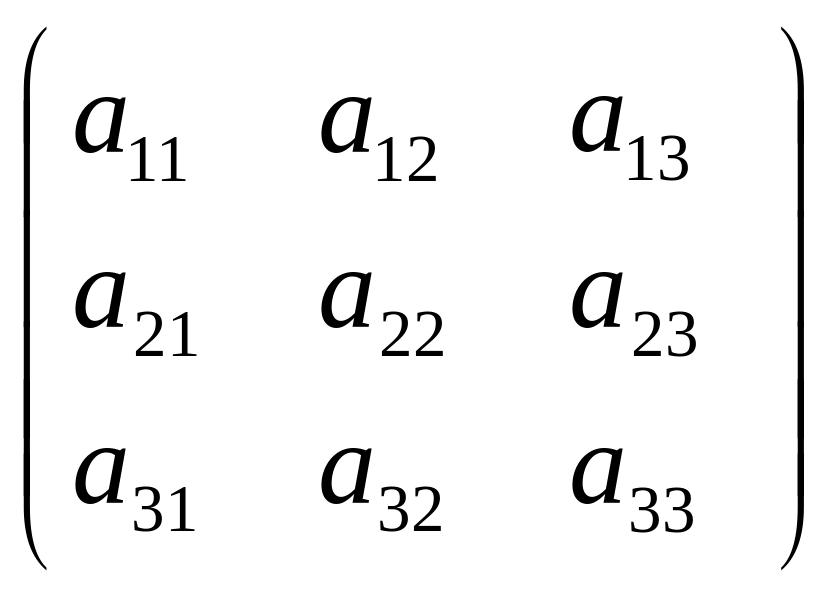 называется число

.

Для вычисления определителей порядка большего трех вводят понятие алгебраического дополнения для элемента .

Определение. Алгебраическим дополнением элемента квадратной матрицы -го порядка называется произведение числа на определитель -го порядка, получающийся вычеркиванием в матрице строки и столбца в которых расположен элемент ( -ой строки и -го столбца).

Пример. Вычислим алгебраические дополнения элементов и матрицы 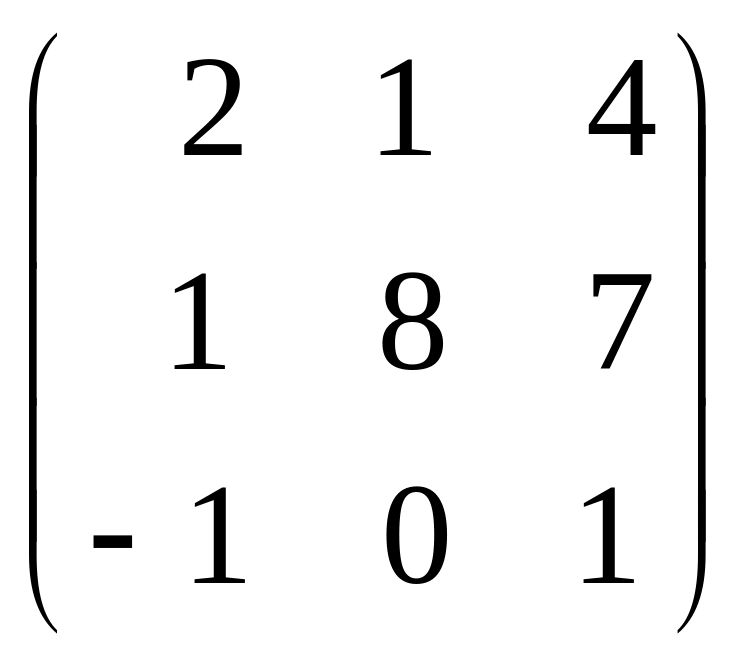. По определению ;

Определение. Определителем матрицы -го порядка называется сумма произведений элементов первой строки матрицы на их алгебраические дополнения: .

Квадратная матрица называется неособенной (невырожденной), если ее определитель не равен нулю, и особенной (вырожденной), если ее определитель равен нулю.

Замечание. Из определения следует, что при определитель -го порядка сводится к вычислению определителей -го порядка, которые в свою очередь последовательно сводятся к определителям 3-го порядка.

Теорема (Лапласа). Определитель матрицы -го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

.

Задача. Доказать, что определитель единичной матрицы любого порядка равен 1.

Задача. Доказать, что определитель диагональной матрицы равен произведению чисел на главной диагонали.

Для квадратной матрицы

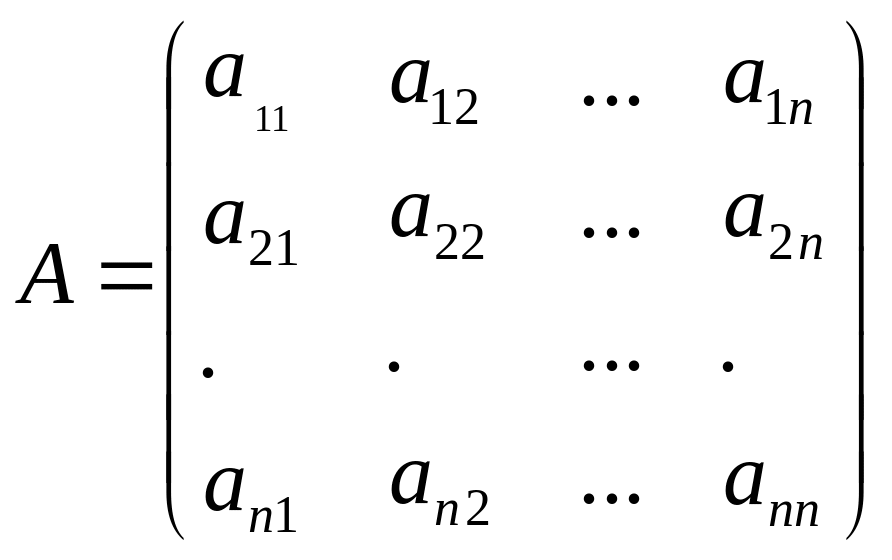(1)

составим матрицу из алгебраических дополнений матрицы :

.

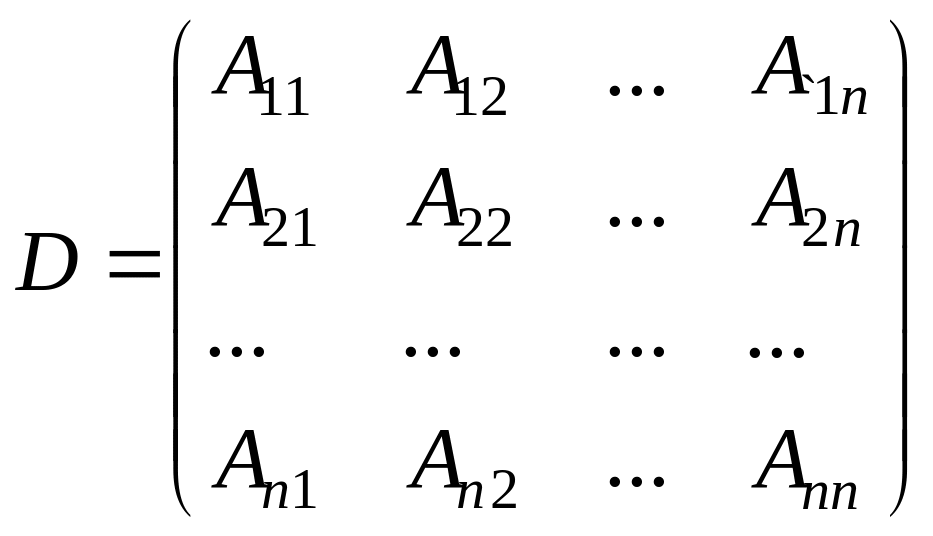Определение. Матрица (транспонированная матрица ) называется присоединенной для квадратной матрицы .

Теорема. Определитель произведения двух квадратных матриц равен произведению определителей, то есть, если , то .