Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального

образования «Нижегородский государственный университет

им. Н.И. Лобачевского»

Факультет вычислительной математики и кибернетики

Кафедра: Центр прикладной информатики

Специальность: Прикладная информатика (в информационной сфере)

Зачетная работа по курсу «Мониторинг и маркетинг информационных товаров и услуг»

Тема:

«Метод дискриминантного анализа и его применение»

Выполнил:

студент группы 85-06 Огородников К.Г.

Преподаватель:

доцент, к.х.н. Кузенкова Г.В.

Нижний Новгород

2012

Содержание

1. Основы дискриминантного анализа 5

2. Модель дискриминантного анализа 6

2.1. Определение коэффициентов дискриминантной функции 6

3. Статистики, связанные с дискриминантным анализом 9

4. Выполнение дискриминантного анализа 11

4.1. Формулирование проблемы 11

4.2. Определение коэффициентов дискриминантной функции 12

4.3. Определение значимости дискриминантной функции 13

4.4. Интерпретация результатов 14

4.5. Оценка достоверности дискриминантного анализа 15

5. Использование в специализированных программах 16

6. Резюме 17

7. Пример использования метода 19

Заключение 24

Список литературы 25

Исходная информация в социально-экономических исследованиях представляется чаще всего в виде набора объектов, каждый из которых характеризуется рядом признаков (показателей). Поскольку число таких объектов и признаков может достигать десятков и сотен, и визуальный анализ этих данных малоэффективен, то возникают задачи уменьшения, концентрации исходных данных, выявления структуры и взаимосвязи между ними на основе построения обобщенных характеристик множества признаков и множества объектов. Такие задачи могут решиться методами многомерного статистического анализа.

Многомерный статистический анализ - раздел математической статистики, посвященный математическим методам, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенным для получения научных и практических выводов.

Основное внимание в многомерном статистическом анализе уделяется математическим методам построения оптимальных планов сбора, систематизации и обработки данных, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенным для получения научных и практических выводов.

Исходным массивом многомерных данных для проведения многомерного анализа обычно служат результаты измерения компонент многомерного признака для каждого из объектов исследуемой совокупности, т.е. последовательность многомерных наблюдений. Многомерный признак чаще всего интерпретируется как величина случайная, а последовательность наблюдений как выборка из генеральной совокупности. В этом случае выбор метода обработки исходных статистических данных производится на основе тех или иных допущений относительно природы закона распределения изучаемого многомерного признака.

По содержанию многомерный статистический анализ может быть условно разбит на три основных подраздела:

1. Многомерный статистический анализ многомерных распределений и их основных характеристик охватывает ситуации, когда обрабатываемые наблюдения имеют вероятностную природу, т.е. интерпретируются как выборка из соответствующей генеральной совокупности. К основным задачам этого подраздела относятся: оценивание статистическое исследуемых многомерных распределений и их основных параметров; исследование свойств используемых статистических оценок; исследование распределений вероятностей для ряда статистик, с помощью которых строятся статистические критерии проверки различных гипотез о вероятностной природе анализируемых многомерных данных.

2. Многомерный статистический анализ характера и структуры взаимосвязей компонент исследуемого многомерного признака объединяет понятия и результаты, присущие таким методам и моделям, как регрессионный анализ, дисперсионный анализ, ковариационный анализ, факторный анализ и т.д. Методы, принадлежащие к этой группе, включают как алгоритмы, основанные на предположении о вероятностной природе данных, так и методы, не укладывающиеся в рамки какой-либо вероятностной модели (последние чаще относят к методам анализа данных).

3. Многомерный статистический анализ геометрической структуры исследуемой совокупности многомерных наблюдений объединяет понятия и результаты, свойственные таким моделям и методам, как дискриминантный анализ, кластерный анализ, многомерное шкалирование. Узловым для этих моделей является понятие расстояния, либо меры близости между анализируемыми элементами как точками некоторого пространства. При этом анализироваться могут как объекты (как точки, задаваемые в признаковом пространстве), так и признаки (как точки, задаваемые в объектном пространстве).

Прикладное значение многомерного статистического анализа состоит в основном в решении следующих трех задач:

• задача статистического исследования зависимостей между рассматриваемыми показателями;

• задача классификации элементов (объектов или признаков);

• задача снижения размерности рассматриваемого признакового пространства и отбора наиболее информативных признаков.

Множественный регрессионный анализ предназначен для построения модели, позволяющей по значениям независимых переменных получать оценки значений зависимой переменной.

Логистическая регрессия для решения задачи классификации. Это разновидность множественной регрессии, назначение которой состоит в анализе связи между несколькими независимыми переменными и зависимой переменной.

Факторный анализ занимается определением относительно небольшого числа скрытых (латентных) факторов, изменчивостью которых объясняется изменчивость всех наблюдаемых показателей. Факторный анализ направлен на снижение размерности рассматриваемой задачи.

Кластерный и дискриминантный анализ предназначены для разделения совокупностей объектов на классы, в каждый из которых должны входить объекты в определенном смысле однородные или близкие. При кластерном анализе заранее неизвестно, сколько получится групп объектов и какого они будут объема. Дискриминантный анализ разделяет объекты по уже существующим классам.

1. Основы дискриминантного анализа

Дискриминантный анализ (discriminant analysis) используется для анализа данных в том случае, когда зависимая переменная категориальная, а предикторы (независимые переменные) интервальные.

Например, зависимая переменная может быть выбором торговой марки персонального компьютера (торговые марки А, В или С), а независимыми переменными могут быть рейтинги свойств персональных компьютеров, измеренные по семи бальной шкале Лайкерта.

Дискриминантный анализ преследует такие цели:

1. Определение дискриминантных функций (discriminant functions) или линейных комбинаций независимых переменных, которые наилучшим образом различают (дискриминируют) категории (группы) зависимой переменной;

2. Проверка существования между группами значимых различий с точки зрения независимых переменных;

3. Определение предикторов, вносящих наибольший вклад в межгрупповые различия;

4. Отнесение случаев к одной из групп (классификация), исходя из значений предикторов;

5. Оценка точности классификации данных на группы.

Метод дискриминантного анализа описывается числом категорий, имеющихся у зависимой переменной. Если она имеет две категории, то метод называют дискриминантным анализом для двух групп (two-group discriminant analsysis).

Если анализируют три или больше категорий, то метод называют множественным дискриминантным анализом (multiple descriminant analysis).

Главное отличие между ними заключается в том, что при наличии двух групп возможно вывести только одну дискриминантную функцию. Используя множественный дискриминантный анализ, можно вычислить несколько функций.

2. Модель дискриминантного анализа

Модель дискриминантного анализа (discriminant analysis model) имеет следующий вид:

,

где D – дискриминантный показатель (дискриминант), b – дискриминантный коэффициент или вес, X – предиктор или независимая переменная.

Коэффициенты или веса (b) определяют таким образом, чтобы группы максимально возможно отличались значениями дискриминантной функции. Это происходит тогда, когда отношение межгрупповой суммы квадратов к внутри групповой сумме квадратов для дискриминантных показателей максимально. Любая другая линейная комбинация предикторов приводит к меньшему значению этого отношения. Технические детали вычисления описаны в подразделе 2.1. С дискриминантным анализом связан ряд статистик, описанный в разделе 3.

2.1. Определение коэффициентов дискриминантной функции

Предположим, что имеется G групп, , каждая из которых содержит наблюдений по независимым переменным, . Введем следующие условные обозначения:

– общий размер выборки;

– матрица скорректированных на среднее значение суммы квадратов и векторных произведений для группы;

– матрица суммарных скорректированных на среднее значение суммы квадратов и векторных произведений;

– матрица скорректированных на среднее значение межгрупповых суммы квадратов и векторных произведений;

– матрица суммарных скорректированных на среднее значение межгрупповых суммы квадратов и векторных произведений для всех N наблюдений;

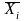– вектор средних значений наблюдений в группе;

– вектор общей средней для всех N наблюдений;

– отношение межгрупповой суммы квадратов к внутригрупповой сумме квадратов;

– вектор дискриминантных коэффициентов или весов.

Тогда

Определим линейный составной компонент . Тогда, с учетом , межгрупповые и внутригрупповые суммы квадратов задаются выражениями и соответственно. Для того чтобы максимально различить (дискриминировать) группы, определяют дискриминантные функции, чтобы максимизировать межгрупповую изменчивость. Коэффициенты рассчитывают так, чтобы максимизировать решением уравнения

Взяв частную производную по и приравняв ее нулю, после некоторых упрощений получим:

Чтобы проще найти , умножим все выражение на и решим следующее характеристическое уравнение:

Максимальное значение – это наибольшее собственное значение матрицы , а – соответствующий собственный вектор матрицы. Элементы – это дискриминантные коэффициенты или веса, соответствующие первой дискриминантной функции. В целом можно определить меньше, чем ( ) или k дискриминантных функций, каждую с соответствующим ей собственным значением. Дискриминантные функции оценивают последовательно. Другими словами, первая дискриминантная функция вносит самый большой вклад в межгрупповую изменчивость. Вторая функция максимизирует межгрупповую вариацию, которая не объяснена первой функцией и т.д.