1 .5. Классификация кристаллов по типу связей.

Расположение атомов или молекул в кристалле зависит от сил взаимодействия между ними. Частицы располагаются таким образом, чтобы энергия взаимодействия между ними была минимальной. Положительная разность между энергией изолированных атомов и атомов в кристаллической решетке называется энергией связи. Значения энергии связи колеблются от 0,1 до 7 эВ на частицу в зависимости от характера взаимодействия. Энергия связи определяет работу, необходимую для удаления частицы из кристалла. Классифика­ция кристаллов по типам связи следующая:

1. Кристаллы с ван-дер-ваальсовскими связями или молекулярные кристаллы.

Силы взаимодействия в таких кристаллах определяются наличием у молекул естественных или индуцированных электрических моментов. Энергия связи молекулярных решеток обычно имеет порядок 10³ ... 10⁴ Дж/моль. Пример таких кристаллов – затвердевшие инертные газы (неон, аргон, криптон, ксенон). Тип решетки этих кристаллов – гранецентрированная кубическая. В ней каждый атом имеет 12 соседей.

2. Кристаллы с ковалентпной связью. В них взаимодействие между частицами обусловлено тем, что два электрона принадлежат одновременно двум атомам. Такая связь называется также валентной или гомеополярной. Энергия связи таких кристаллов составляет порядка 10⁵… 10⁶ Дж/моль. Примеры - кремний, алмаз и др. Кристаллы с такими связями часто встреча-ются в различных структурных модификациях с почти одинаковыми энергиями связи. Такие модификации называются аллотропными.

3. Кристаллы с водородной связью, образующейся благодаря электри-ческому взаимодействию атома водорода с другими атомами, обладающими значительной электроотрицательностью. Энергия этой связи достигает 10⁴ Дж/моль. Типичный пример – кристаллы льда, фтороводород HF, синильная кислота HCN и др.

4. Кристаллы с ионной связью, или просто ионные кристаллы, состоят из ионов противоположных знаков, располагающихся в узлах кристалличес-кой решетки. Энергия связи в таких кристаллах определяется силой кулоновс-кого взаимодействия и достигает величины 10⁵... 10⁶ Дж/моль. Типичный пример NaCl, NH₄F и др.

5. Кристаллы с металлической связью представляют собой совокуп-ность положительных ионов, располагающихся в узлах кристаллической решетки, между которыми квазисвободно движутся валентные электроны, обеспечивая взаимодействие между ионами. Энергия связи в металлических кристаллах составляет 10⁴…10⁵ Дж/моль. Как уже указывалось, кроме вы-шеназванных, между частицами в кристалле возможны смешанные связи.

1.6.Символические обозначения плоскостей и направлений в кристаллах. Индексы Миллера.

Анизотропия кристаллов приводит к необходимости выделять и оп­ределенным образом обозначать различные плоскости и направления в кристалле. Для этого пользуются специальной системой координат, связанной с кристаллом так, что координатные оси оказываются параллельными осям симметрии кристалла или перпендикулярными плоскостям симметрии. Координаты в такой системе измеряются в единицах, равных межатомным расстояниям в данном направлении. Эти расстояния называются еще постоянными решетки или параметрами решетки. Положение какой-либо плоскости однозначно определяется координатами любых трех точек этой плоскости, например тех, в которых плоскость пересекается осями координат (рис.1.6.1).

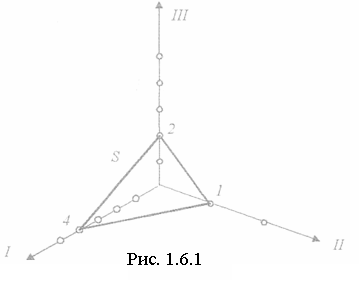
Пусть оси I, II и III являются координатными осями и нуж-но определить плоскость S. Если, например, плоскость пе-ресекает ось I в точке на расстоянии в 4 единицы (т.е. 4 межатомных расстояния), ось II на расстоянии в 1 единицу и ось III на рас-стоянии в 2 единицы, то положение плоскости задается тройкой чисел 4,1,2. Однако в кристаллографии принято пользоваться для обозначения плоскостей не этими числами, а особыми индексами Миллера, которые определяются следующим образом. Берутся обратные значения полученных координат точек пересечения плоскостью координатных осей и эти дроби приводятся к одному знаменателю. Знаменатель отбрасывается, а числители полученных дробей и дают индексы Миллера. Для рассмотренного на чертеже примера координаты равны 4,1,2. Их обратные значения дадут дроби 1/4; 1/1; 1/2. Общий знаменатель дробей – 4. Числители или индексы Миллера оказываются равными 1, 4, 2. Эти индексы записываются в круглых скобках и читаются раздельно (142). Такой набор индексов определяет не одну плоскость, а все семейство параллельных плоскостей. Если рассматриваемая плоскость параллельна одной из осей, т.е. пересекает ее в бесконечности, то соответствующий индекс равен нулю. На рисунке 1.6.2 указаны индексы наиболее важных плоскостей кубического кристалла.

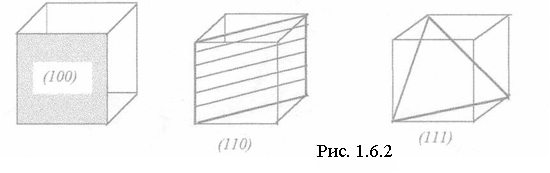
Направления в кристалле также задаются индексами, которые определяются следующим образом. Вдоль определяемого направления выбирают некоторый вектор произволь­ной длины и определяют величины составляющих вектора по осям координат в единицах постоянной решетки. Тогда индексами этого направления будут три наименьших целых числа, отношения которых между собой равны отношениям составляющих вектора. Если компоненты вектора равны, например 6, 4, 8 единицам, то индексами соответствующего этому вектору направления будут 3,2, и 4. Эти числа заключаются в квадратные скобки [324].