1.4. Классы симметрии. Решетка Браве.

Классы симметрии. Различные кристаллы могут обладать несколькими элементами симметрии. Очевидно, что, чем большим числом элементов симметрии обладает тело, тем оно симметричнее. Шар, обладающий бесконечным числом осей симметрии, плоскостей симметрии и центром симметрии, является наиболее симметричным телом. В кристаллографии показано, что существуют всего 32 возможные комбинации элементов симметрии. Каждая из таких возможных комбинаций называется классом симметрии. В природе существуют только кристаллы, относящиеся к одному из 32 классов симметрии. Например, кристаллы, обладающие одной осью симметрии, образуют пять классов симметрии из 32-х, соответствующих пяти порядкам этих осей, включая и ось первого порядка, когда симметрии нет.

Четыре класса образуют кристаллы, обладающие кроме указанной оси симметрии еще и перпендикулярными к ней осями второго порядка. Отдельный класс симметрии образуют кристаллы, обладающие только центром симметрии, и т.д.

В кристаллографии принято объединять 32 класса симметрии в 7 систем симметрии или 7 сингоний, которые носят следующие названия в порядке возрастания симметрии:

• триклинная система, включающая два класса симметрии,

• тригональная система, объединяющая семь классов,

• моноклинная система, куда входят три класса.

• гексагональная система - пять классов,

• ромбическая, также с тремя классами,

• тетрагональная система с семью классами,

кубическая система., наиболее симметричная, включающая пять классов.

Э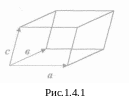 лементарная ячейка триклинной сингонии показана на рис.1.4.1. Решетка такого типа обладает низшей симметрией. Стороны параллелепипеда образованы разными ортами вектора трансляции. Углы между ортами также разные.

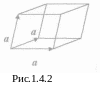
Тригоналъной решетке (рис.1.4.2) соответст-вует ячейка, образованная равными по модулю векторами, углы между которыми также равны друг другу.

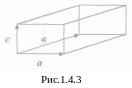
Моноклинная решетка (рис.1.4.3) состоит из ячеек, образованных тремя разными вектора-ми, один из которых образует прямой угол с двумя другими.

Г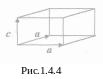 ексагональная решетка (рис. 1.4.4) состоит из элементарных ячеек, стороны которых образованы двумя одинаковыми векторами, угол между которыми равен 60° и третьим вектором, перпендикулярным к двум другим и неравным им по модулю.

В ромбической решетке (рис. 1.4.5) элементарная ячейка образована неравны-ми друг другу векторами, углы между которыми – прямые. В ячейке тетра-гональной решетки (рис.1.4.6) углы между векторами сохраняются прямыми, но только два вектора равны друг другу по модулю, и, наконец, в кубической решетке элементарная ячейка (рис.1.4.7) образована тремя равными по модулю векторами, ортогональными друг другу.

Следует отметить, что в кристалле частицы вещества (атомы, ионы или молекулы) могут располагаться не только в узлах кристаллической решетки, но и в центре граней (гране-центрированная решетка) или в середине диагональной плоскости, проходящей через вершины (объемно-центрированная решетка), С учетом такого расположения частиц можно сформировать 14 трехмерных решеток, названных решетками Браве.