§2. Отношение порядка на множестве действительных чисел.

Опр.1. Отношением порядка называется рефлексивное, антисимметричное и транзитивное отношение на множестве.

Опр.2. Линейно упорядоченное множество называется плотным, если для любых разных элементов этого множества элемент, который находится между ними.

Теорема 1: Отношение «больше» на множестве действительных чисел является отношением строгого линейного порядка.

Док-во:

• Рефлексивность:

• Антисимметричность:

• Транзитивность:

Пусть n = max{k,m}, тогда .

• Линейность: отношение порядка называется линейным, если .

Свойство 1: На множестве D отношение порядка согласуется с отношением порядка на множестве рациональных чисел.

Док-во:

.

Так как в D дроби имеют конечную длину, то это же отношение выполняется и на D.

Ч.т.д.

§3. Плотность множества действительных чисел.

Теорема 1. Множество D плотно в множестве действительных чисел, т.е. между любыми двумя не равными действительными числами находится конечная десятичная дробь.

Доказательство:

2.

3.

1. такое n по определению отношения “<”. 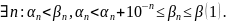Покажем, что дважды равенство получится не может ОП: , начиная с какого-то n, тогда:

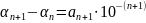
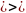
= 9, начиная с некоторого индекса, а это невозможно по определению R числа ?! Таким образом, (1) одно из нестрогих неравенств является строгим для некоторого индекса n, тогда равенство

2. Между 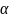и находится 0, а это конечная десятичная дробь.

3. 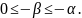 Согласно первому случаю такая конечная десятичная дробь , что , а следовательно . ч.т.д.

Следствие: Пусть последовательность, где каждое десятичная дробь с n знаками после запятой. И пусть 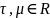такие, что:

Доказательство: Пусть .

t

S

по предыдущей теореме из того, что => конечные десятичные дроби s и t, что , тогда - = 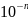, . !? (противоречит архимедовости).

§4. Десятичные приближения

Определение 1: Пусть  - десятичная дробь. Десятичным приближением числа  порядка n называется число u_n()=

Примеры:

1)=0,01234…

₁=0,0=0= u₁()

₂=0,01= u₂()

₃=0,012= u₃()

₄=0,0123= u₄()

u₁()=-0,0-10^-1= -0,1

2)=a₀,a₁a₂…a_n

_k=a₀,a₁a₂…a_k k-ая подходящая дробь

u₂()=₂-10^-2=-0,01-10^-2=-0,02

u₃()=₃-10^-3=-0,012-10^-3=-0,013

u₄()=₄-10^-4=-0,0123-10^-4=-0,0124

u_n()<<u_n()+10^-n

Свойство 1: R : u_n()u_n+1()

Свойство 2: ,R  1)<n : u_n()<u_n()

2) n : u_n()u_n()

§5 Теорема о точной верхней границе

Опр. Пусть M – упорядоченное мн-во, А – непустое подмн-во мн-ва М. Эл-т наз. верхней границей мн-ва А, если вып-ся: .

Подмножество А, кот. имеет верхн.границу. наз. ограниченным сверху.

Точной вер. границей мн-ва А (sup A) наз. наименьшая из верхних границ множества А., наз. нижней границей мн-ва А, если .

Подмножество А, которое имеет нижнюю границу наз. ограниченным снизу.

Точной нижней границей множества А наз. наибольшая из нижних границ множества А.

Св-ва 1. Пусть , тогда:

1. 

2. 

Док-ва сам.

Св-ва 2. Пусть А – подм-во мн-ва М и . Пусть В – мн-во всех вершин границ мн-ва А, тогда

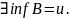
Теорема (о точной верхней границе). Каждое ограниченное сверху (снизу) подм-во мн-ва действ. чисел имеет точную верхнюю (нижнюю) границу.