Практическое занятие № 5

Тема: Статистические индексы.

Введение: Характеристика цели занятия: изучение алгоритма расчета статистических индексов, методы построения агрегатных индексов.

Вопросы для обсуждения:

• Общее понятие об индексах.

• Виды индексов.

• Использование индивидуальных индексов в экономическом анализе.

• Формы представления общих индексов.

• Средний гармонический и средний арифметический индексы.

• Взаимосвязь индексов.

• Территориальные индексы.

Материал для выполнения

Задача 1.

Имеются следующие данные о ценах продукта К (таблица 1). Рассчитаете все возможные варианты индивидуальных индексов и сделайте выводы.

Таблица 1

	Сентябрь	Ноябрь	Индивидуальный индекс цен
Розничная цена за 1 кг, грн.	30	40	1,33 или 133 %
Оптовая цена за 1 кг, грн.	20	20	1,0 или 100 %

Вычисленные в последней графе таблицы индивидуальные индексы показывают, что цена 1 кг данного продукта на рынке была в ноябре на 33,3 % выше, чем в сентябре. Оптовая цена не изменилась. Но если требуется определить соотношение розничных и оптовых цен, то индекс ноября исчисляется так:

Это говорит о том, что розничная цена 1 кг продукта К на рынке была в 2 раза выше оптовых цен.

При анализе цен возможна иная постановка вопроса: определить, на сколько процентов оптовая цена 1 кг продукта К была в ноябре ниже розничной цены? Для ответа на этот вопрос за базу сравнения принимается уровень розничной цены:

Вывод: Этот индекс показывает, что оптовая цена в ноябре была на 50 % ниже уровня розничной цены (50-100=- 50% - знак «-» указывает на снижение уровня показателя).

Из рассмотренного примера видно, что при вычислении индексов база сравнения имеет непосредственное влияние на показание индекса, а выбор базы сравнения определяется целью исследования.

Задача 2.

Примените индексный метод изучения динамики сложных статистических совокупностей. Сделайте выводы.

Таблица 2

Товар	Единица измерения	1 период		2 период		Индивидуальные индексы
		Цена за единицу, грн	Кол-во	Цена за единицу, грн	Кол-во	цен	физичес-кого объёма
А	т	20	7 500	25	9 500	1,25	1,27
Б	м	30	2 000	30	2 500	1,0	1,25
В	шт.	15	1 000	10	1 500	0,67	1,5

При определении статистических индексов первый период принимается за базисный, второй – за отчётный.

Вывод: 1. Индивидуальные (однотоварные) индексы показывают, что в текущем периоде по сравнению с базисным цена на товар А повысилась на 25 %, на товар Б – осталась без изменений, а на товар В – снизилась на 33 %.

2. Количество реализации товара А возросло на 27 %, товара Б – на 25 %, а товара В – на 50 %.

Разновеликие по направлению и интенсивности изменения индивидуальных индексов обусловливают необходимость при их обобщении определения общего для данного ассортимента изменения цен и количества реализованных товаров. Для этого вычисляются агрегатные индексы Пааше и Ласпейреса.

Числитель индекса Пааше:

Знаменатель:

Вывод: По данному ассортименту товаров в целом цены повысились в среднем на 13,9 %.

Числитель индекса Ласпейреса:

Знаменатель индексного соотношения:

Вывод: По ассортименту в целом повышение цены составило в среднем 14,4 %.

Расчёты имеют различные показания индексов цен, что объясняется тем, что индексы Пааше и Ласпейреса характеризуют различные качественные особенности изменения цен.

Пример. Определим общий индекс цен по данным таблицы 2 о продаже товаров в магазине.

С помощью агрегатных индексов можно определить не только относительное изменение явления, но и абсолютные размеры этого изменения. Разница между числителем и знаменателем агрегатного индекса характеризует абсолютное изменение сложного явления за счёт индексированной величины.

Задача 3.

По имеющимся данным рассчитайте агрегатный индекс цен и физического объёма продукции, а также изменения, вызванные колебаниями цены и объёма.

Таблица 2

Товар	Продажа в ценах соответствующего периода, тыс. грн		Изменение цен в текущем периоде по сравнению с базисным, %	Расчётные графы
	базисный	текущий
1	2	3	4	5	6
А	153,5	185,0	-4	0,96	192,7
Б	245,0	260,6	+10	1,1	236,9
В	21,5	29,4	без изменения	1,0	29,4
Итого	420,0	475,0	х	х	459,0

В графе 5 определены индивидуальные (однотоварные) индексы цен.

В графе 6 по каждому товару исчислены отношения стоимости продажи товаров в текущем периоде к индивидуальному индексу цен. Например, 185:0,96=192,71 тыс. грн. и т. д.

Итоговые данные подставляются в формулу среднегармонического индекса:

Вывод: По данному ассортименту в текущем периоде цены повышены в среднем на 3, 5%.

Если в формуле (1) из числителя вычесть знаменатель, то получают показатель прироста товарооборота в текущем периоде в результате изменения цен:

. (2)

Для данных табл. 1 прирост товарооборота в текущем периоде в результате изменения цен составит:

475,0-459,0=16,0 тыс. грн, то есть объём товарооборота возрос на 16,0 тыс. грн.

Полученное в итоге графы 6 (табл. 1) значение может быть использоваться для определения общего индекса физического объёма товарооборота в сопоставимых (базисных) ценах. Для этого применим формулу:

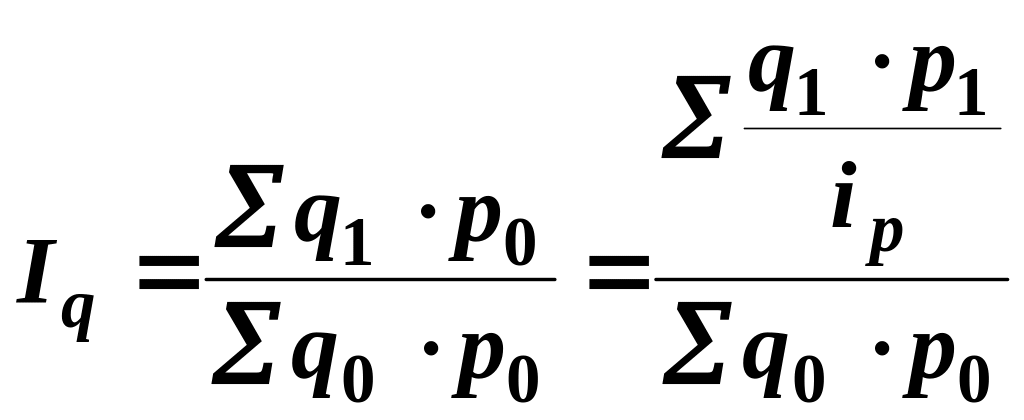(3)

При этом - индивидуальный индекс цен.

Подставляя в формулу (3) итоговые данные граф 2 и 6 табл. 1, вычисляем:

.

Вывод: Физический объём продажи товаров увеличился в текущем периоде в среднем на 9,3 %.

На основе формулы (3) исчисляется прирост суммы товарооборота в текущем периоде в результате изменения физического объёма продажи товаров:

(4)

Подставляя числовые значения: 459,0 – 420,0 =39,0 тыс. грн.

Общий вывод по примеру: Индексный анализ табл. 2 показал, что снижение цен по ассортименту в целом в среднем на 3,5 % вызвало увеличение товарооборота на 16,0 тыс. грн. Увеличение физического объёма продажи товаров в среднем на 9.3 % обусловило рост товарооборота на 39,0 тыс. грн. В результате совокупного действия этих факторов прирост объёма товарооборота в текущих ценах составил 55.0 тыс. грн. (39,0+16,0=55,0 тыс. грн.). Это соответствует расчёту по формуле:

тыс. грн. – то есть расчёты проведены правильно.

Задача № 4.

Имеются следующие данные о заготовке фруктов:

Год	2005	2006	2007	2008	2009	2010
Год	1997	1998	1999	2000	2001	2002
Кол-во фруктов, тыс. т	20	24	26	30	31	37

Исчислите цепные и базисные индивидуальные индексы объема заготовок фруктов и проверьте их результаты, используя взаимосвязь цепных и базисных индексов.