2.3 Пример расчета сложной цепи разными методами

Задача:

Рис.2.5

Д ва источника питания с э. д. с. Е₁ = 60 В и Е₂ = 75 В включены в схему, как показано на рис. 2.5. Найти токи, протекающие через сопротивление резисторов, если

R₁ = 2 Ом; R₂ = 3 Ом; R₃ = 5 Ом. Сопротивлением источников питания Е₁ и Е₂ пренебречь.

С помощью законов Кирхгофа

1. В данной схеме (рис.2.6) два узла (1 и 2), три ветви (первая содержит е1, r1; вторая – е2, r2, третья - r3 ) и два контура (первый содержит е1, r1, r3; второй содержит е2, r2 ,r3 ).

Рис.2.6

2. Согласно направлению э. д. с. Е₁,Е₂ выбираем направление токов в схеме по часовой стрелке (см. рис.2.6).

3. Уравнение для узла 1 на основании первого закона Кирхгофа

I₂ +I₃ - I₁ = 0

4. Уравнения для контуров на основании второго закона Кирхгофа. Для первого контура Е₁ = U₁ + U₃ или Е₁= I₁R₁ +I₃R₃.

21

Для второго контура Е₂= U₂ - U₃ или Е₂ = I₂R₂ - I₃R₃.

5. Решаем систему уравнений, определяем значения токов, протекающих по ветвям схемы.

I₂ +I₃ - I₁ = 0 I₁ = 27,6 А

Е₁= I₁R₁ +I₃R₃ 7I₁ - 5I₂ = 60 I₂ = 26,6 А

Е₂ = I₂R₂ - I₃R₃ 8I₂ - 5I₁ = 75 I₃ = 1 А.

М етод контурных токов

Рис.2.7

1. В данной схеме два контура: первый содержит Е₁, R₁, R₃; второй содержит Е₂, R₂ ,R₃ (рис 2.7). Значит необходимо найти два контурных тока и для решения необходимо составить два уравнения.

2. Направление обхода тока по каждому контуру выбираем по часовой стрелки ( см. рис2.7).

3. Составляем уравнения для каждого контура на основании второго закона Кирхгофа.

Для первого контура: Е₁ = U₁ + U₃ или Е₁ = I_IR₁ + (I_I -I_II) R₃

Для второго контура: Е₂ = U₂ + U₃ или Е₂ = I_{I I}R₂ + (I_{I I} -I_I) R₃

4. Решая систему уравнений, вычисляем значения токов II , III, протекающих по каждому контуру схемы

Е₁ = I_IR₁ + (I_I -I_II) R₃ 60 = 2 ∙I_I +5∙( I_I -I_II) 7I_I - 5I_II = 60 I_I =27,6 А

Е₂ = I_{I I}R₂ + (I_{I I} -I_I) R₃ 75 = 3∙I_I + 5∙( I_II - I_I ) 8I_II - 5I_I = 75 I_II = 26,6 А

В соответствии с принятыми обозначениями определяем токи, проходящие через потребителей I₁ = I_I =27,6А ; I₂ = I_II = 26,6А ; I₃ = I_I -I_II =1А.

Метод наложения

1. В схеме два э. д. с., поэтому схема разбивается на две (рис.2.8).

22

2. Принимаем э. д. с. Е₂=0 и схема преобразовывается в сему на рис.2.8,а.

3. Согласно направлению э. д. с. Е₁ задаем направление токов по ветвям.

а) б)

Рис.2.8

4. Определяем эквивалентное сопротивление схемы. R₁ соединено последовательно с R₂ и R₃ , которые соединены параллельно. Эквивалентное сопротивление равно

R_э1= R₁ + =3,875 Ом.

5. Определяем токи ветвей I₁₁, I_12, I₁₃.

I₁₁ = =15,5А.

Падение напряжения на R₁ равно U₁₁ = I₁₁∙ R₁=15,5∙2 = 31В.

Т.к. Е₁ = U₁₁+ U_1(1-2), то U_1(1-2) = 60 - 31 = 29В.

Резисторы R₂ и R₃ соединены параллельно, то U_1(1-2) =U₁₂= U₁₃.

Определяем токи через резисторы R₂ и R₃

I₁₂ = =9,6А; I₁₃ = 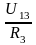= 5,9А.

Расчет для схемы с э. д. с. Е₂ аналогичен (рис 2.8,б).

Определяем эквивалентное сопротивление схемы. R₂ соединено последовательно с R₁ и R₃ , которые соединены параллельно. Эквивалентное сопротивление равно

R_э2= R₂ + = 4,4 Ом.

23

Определяем токи ветвей I₂₁, I_22, I₂₃.

I₂₂ = =17 А.

Падение напряжения на R₂ равно U₂₂ = I₂₂∙ R₂=17∙3 = 51В.

Т.к. Е₂ = U₂₂+ U_2(1-2), то U_2(1-2) = 75 - 51 = 24 В.

Резисторы R₁ и R₃ соединены параллельно, то U_2(1-2) =U₂₁= U₂₃. Определяем токи через резисторы R₁ и R₃

I₂₁ = = 12,1А; I₁₃ = = 4,9А.

Учитывая направления токов на рис. 2.8, а, б, определяем искомые токи, как алгебраические суммы

I₁ = I₁₁+ I₁₂ = 27,6 А; I₂ = I₁₂ + I₂₂ = 26,6 А; I₃ = I₁₃— I₂₃= 1 А.