1.1 Цель работы

Расширить знания об электрических цепях, закрепить навыки расчёта параметров смешанных схем, определение электрических характеристик элементов.

1.2 Теоретические сведения

Электрическая цепь называется линейной, если она содержит только линейные элементы. Линейным называется элемент цепи, сопротивление которого остается постоянным независимо от силы тока в нём и от величины напряжения на его зажимах.

Узлом электрической цепи называется соединение трёх и более проводов.

Рис.1.1 Последовательное соединение

с оединение элементов Если несколько резисторов (или приёмников энергии) соединены один за другим без разветвлений и по ним протекает один и тот же ток, то они образуют одну ветвь и соединение резисторов называется последовательным (рис.1.1).

I_AB=I_BC=I_AC ; U_AB=I_AB·R₁ ; U_BC=I_BC·R₂ ;

U_AC= U_AB+U_BC; U_AC =I_AC·(R₁+R₂)=I_AC·R;

I = I₁ =I₂

U = U₁+U₂ (1.1)

R = R₁+R₂

При последовательном соединении линейных отдельных элементов (R₁,R₂) электрический ток них один и тот же. Между входными зажимами действует напряжение U, которое равно сумме падений напряжения на отдельных элементах U₁ и U₂. Ряд последовательно соединённых резисторов R₁ и R₂ можно заменить эквивалентным (общим) сопротивлением R.

9

Используя закон Ома , можно записать:

(1.2)

Т .е. мощность развиваемая в последовательно соединённых резисторах или в эквивалентном резисторе равна сумме мощностей всех резисторов.

Параллельным соединением резисторов (или приёмников энергии) называется такое соединение, при котором к одним и тем же узлам электрической цепи присоединено несколько резисторов (рис.1.2).

Рис.1.2 Параллельное соединение

элементов

Так как резисторы присоединены к одним и тем же узлам, то каждый из них находится под одинаковым напряжением U. Согласно закону Ома токи в резисторах определяются по формулам:

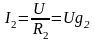(1.3)

I₁, I₂ – токи через элементы, А;

R₁, R₂ – активное сопротивление элементов, Ом;

g₁, g₂ – проводимость элементов, См: т.е. токи в параллельных ветвях с резисторами распределяются прямопропорционально их проводимостям и о братно пропорционально их сопротивлениям.

Эквивалентная проводимость параллельного соединения резисторов равна сумме проводимостей всех параллельных ветвей.

(1.4)

Рис.1.3 Последовательное упрощение схемы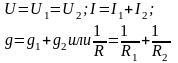

Таким образом, при параллельном соединении (1.5)

10

При расчёте цепи со смешанным соединением резисторов пользуются обычно методом последовательного упрощения или свёртывания схемы.

Например, на рис 1.3.а представлено смешанное соединение четырёх элементов. Элементы 3 и 4 соединены параллельно, последовательно с ними соединены элементы 1 и 2.

При упрощении находим элемент эквивалентный четвёртому и третьему (рис.1.3.б), затем элементы 1, 2 и 3, 4 получаются соединены последовательно. Используя формулы для последовательного соединения (рис.1.3.в), находим эквивалентный элемент 1 – 4.