Расчет производим для соединения звездой

12. Определяем полное сопротивление цепи для каждой фазы при соединении звездой Z_А, Z_В, Z_С с помощью таблицы 8.1.

13. Определяем фазное напряжение по формуле для соединения звездой

Uф=U_А=U_В=U_С= (8.20)

14. Определяем фазный ток на основании закона Ома во всех фазах

для соединения звездой I_А, I_В, I_С по формуле 8.14

I_А= , I_В = , I_С=

15. Определяем угол между током и напряжением для каждой фазы по формуле 8.9

Соsφ_А= , Соsφ_В= , Соsφ_С= . По таблице 8.2 определяем угол φ.

16. Определяем активную мощность трехфазной цепи

а) фазную для соединения звездой

Р_А = I _А·U _АСоsφ _А; Р _В = I _В·U _ВСоsφ _В; Р _С = I _С·U _ССоsφ _С (8.21)

б) трехфазной системы для соединения звездой

Р =Р_А +Р _В +Р _С (8.22)

81

17. Для определения реактивной мощности трехфазной цепи определяем

Sin φ_А= , Sin φ_В= , Sin φ_С= .

18. Определяем реактивную мощность во всех фазах:

Q _А = I _А ·U _А Sinφ _А; Q _В = I _В ·U _В Sinφ _В; Q _С = I _С·U _С Sinφ _С. (8.23)

19. Определяем реактивную мощность трехфазной цепи для соединения звездой

Q = Q _А+ Q _В+ Q _С

20. Определяем полную мощность трехфазной системы для соединения звездой

S = (8.24)

8.4 Пример расчёта

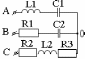
Рис 8.7 К примеру расчета.

Дано: К симметричной трехфазной сети (Рис 8.7) с частотой f=50Гц и линейным напряжением U_л =220В подключен несимметричный приемник энергии, характеризующийся параметрами R, X_L, X_C в фазах. Сопротивлением линейных проводов пренебречь. Определить фазные токи. Числовые значения параметров R₁=10 Ом; R₂=30 Ом; R₃=20 Ом; L₁= 0,08Гн; L₂= 0,16Гн С₁ = 10,62Е-05= 10,62·10^-5Ф. С₂ = 5,31Е-05= 5,31·10^-5Ф.

Решение

1Определяем индуктивное сопротивление цепи по формуле (8.11):

X_L1=ω·L= 2πfL₁= 2·3,14·50·0,08=25,12≈ 25 Ом,

X_L2=ω·L= 2πfL₂= 2·3,14·50·0,16=50,24≈ 50 Ом

82

2. Определяем емкостное сопротивление цепи по формуле (8.12): X_C1= = = Ом;

X_C2= Ом

Расчет производим для соединения треугольником

3. Определяем полное сопротивление цепи для каждой фазы Z_АВ, Z_ВС, Z_СА

Z_АВ = =36 Ом, Z_ВС= = 67 Ом,

Z_СА= =27 Ом

4. Определяем фазное напряжение по формуле (8.13) Uф = Uл

U_АВ= U_ВС=U_СА= Uл = 220В

5. Определяем фазный ток на основании закона Ома во всех фазах: I_АВ, I_ВС, I_СА по формуле (8.14) Iф =

I_АВ= = 220/36 =6,11 А, I_ВС = =220/67=3,28 А,

I_СА= =220 /27 = 8,14А.

6. Определяем угол между током и напряжением для каждой фазы по формуле 8.9

Соsφ_АВ= =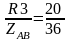 =0,55; Соsφ_ВС= =0,447;

Соsφ_СА= =0,37.

По таблице 8.2 определяем угол φ.

φ_АВ≈ 55°; φ_ВС≈ 65°; φ_СА≈ 70°.

7. Определяем активную мощность трехфазной цепи

а) фазную

Р _АВ = I _АВ ·U _АВ Соsφ _АВ=6,11·220·0,55 = 739,31 Вт

Р _ВС = I _ВС ·U _ВС Соsφ _ВС =3,28·220·0,447 = 322,55 Вт

Р _СА = I _СА·U _СА Соsφ _СА=8,14·220·0,37 = 662,59 Вт;

83

б) трехфазной системы при соединении треугольником

Р∆ =Р _АВ +Р _ВС +Р _СА =739,31+322,55+662,59=1724,46

8. Для определения реактивной мощности трехфазной цепи определяем

Sin φ_АВ= =0,83;

Sin φ_ВС= =0,895;

Sin φ_СА= =0,926.

9. Определяем реактивную мощность во всех фазах:

Q _АВ = I _АВ ·U _АВ Sinφ _АВ=6,11·220·0,83=1115,68 ВАр;

Q _ВС = I _ВС ·U _ВС Sinφ _ВС=3,28·220·0,895 = 645,83 ВАр;

Q _СА = I _СА·U _СА Sinφ _СА= 8,14·220· 0,926 =1658,28 Вар.

10. Определяем реактивную мощность трехфазной цепи

Q∆= Q _АВ+ Q _ВС + Q _СА = 1115,68+645,83+1658,28 = 3043,423 ВАр

11. Определяем полную мощность трехфазной системы для соединения треугольником

S ∆ = 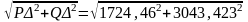= 3498,03 ВА