3. Замена переменных в тройном и n-кратном интеграле
Пусть
задано взаимно-однозначное, непрерывно
- дифференцируемое отображение
 ,
(,
,
)
D
,
(,
,
)
D
из
D
в V,
где области
D
и V
кубируемы. Тогда объема области V
справедлива
формула
V
=
 (4).
(4).
Из
этой формулы и теоремы о среднем следует,
что
 =
V
=
=
V
=
 =
=
D.
D.
Откуда
следует, что в любой точке области M0=(0
,0
,0
)
 =
= .
.
Теорема
( о замене переменных ). Если f
интегрируема в V,
то
 =
=
 .
.
Доказательство.
Интегралы
справа и слева существуют. Выберем
какое-либо разбиение {Dj}
области D
и обозначим
через {Vj}
соответствующее
разбиение области V.
Согласно
формуле (4)
Vj
=
 =
=
Dj.
Dj.
Полученные
таким образом точки Mj
= (j
, j
, j
) будем
рассматривать как промежуточные точки
для интегральных сумм для разбиения
{Dj},
а соответствующие
точки Pj
= (xj
, yj
, zj
) для
интегральных сумм для разбиения {Vj}.
В этом случае
 .
.
Из
этого равенства следует требуемое
утверждение.
Пример
1. Цилиндрические координаты
 ,
x2+y2=z2,
0
z
1
,
x2+y2=z2,
0
z
1
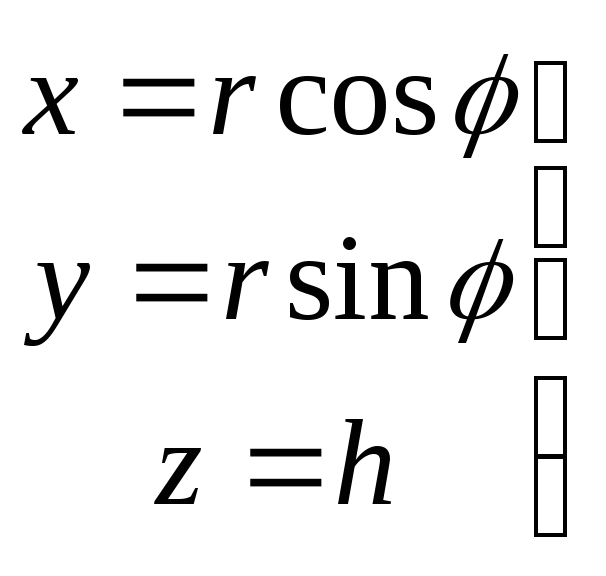 ,
|I| = r.
,
|I| = r.

В
этом случае D
= {(r,,h):
0
2
, 0
r
z
,
z[0,1]}
.
 =
= =
=
 =
=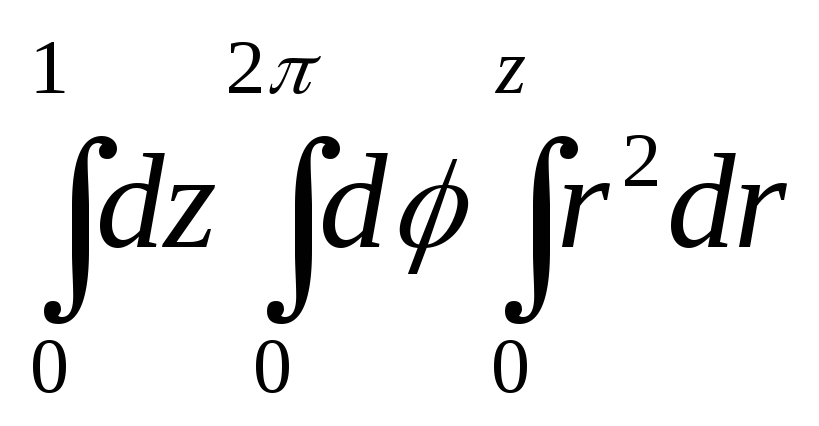 =
= =
= .
.
Пример
2. Сферические координаты
A= ,
x2+y2+z2
1, 0
x , 0
y , 0
z .
,
x2+y2+z2
1, 0
x , 0
y , 0
z .

 ,
|I| = 2cos
.
,
|I| = 2cos
.
A=
4. Замена переменных в общем случае
Рассмотрим
регулярное отображение
 (
кратко x=x(u)
)
(
кратко x=x(u)
)
из
области D
в область
V.
При измеримости
областей D
, V
справедлива
формула замены переменных
 =
= ,
,
существовании
интегралов предполагается.
математический
анализ. 3 семестр. Логинов А.С. 2005 г.
loginov_1999@mail.ru 12


 ,
(,
,
)
D
,
(,
,
)
D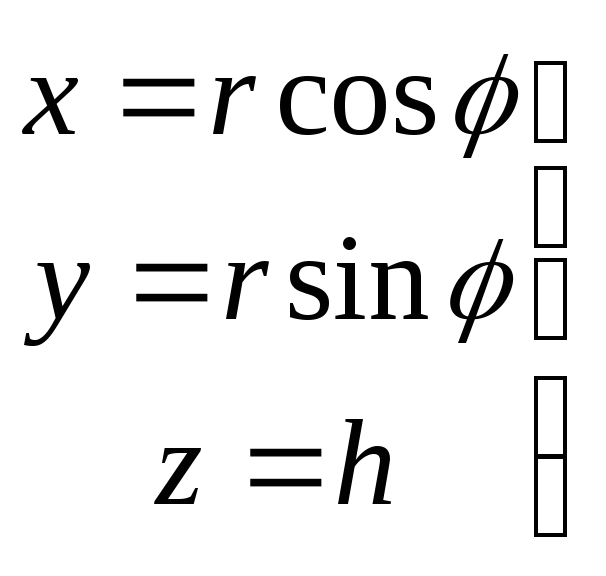 ,
|I| = r.
,
|I| = r.
 =
=
 ,
|I| = 2cos
.
,
|I| = 2cos
. (
кратко x=x(u)
)
(
кратко x=x(u)
)