21. Норм закон распред, его параметры и их вероятностный смысл. Влияние парам а и σ на форму норм кривой.

Норм распред им место,когда наблюд случ велич формир под влиян бол числа случ фактор,ни один из кот сущ-но не превосх остальн.

Непрер случ велич Х имеет норм закон распред(закон Гаусса) с параметрами а и σ², если ее плотность вероятности имеет вид:

К ривую норм закона распред назыв норм или гауссовой кривой.

Н а рис. норм кривая р(х)и граф ф распред случ велич Х

Н орм кривая симм относ прямой х=а, имеет макс в точке х=а, равный и точки перег x=a±σ с ординатой

M(X) =a, D(X) =σ²

Ф распред СВ Х,распр-ной по норм закону,выраж ч/з ф Лапласа

где

В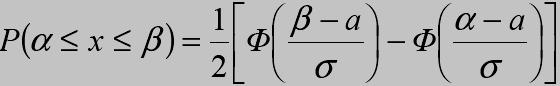 ер попад знач норм случ велич Х в интерв [α,β]опред формул

В ер ,что откл случ велич Х, от мат ожид а не превыс велич ε>0

« Правило трех сигм»:

22. Вероятность попад нормально распред случ величины в заданный интервал: вероятность заданного отклонения.

Вероятность того, что отклонение случ велич Х, распред по норм закону, от мат ожид а не превысит велич ε> 0 (по абсол велич)

23. Правило трех сигм и его знач на практике.

Если случайная велич Х имеет

норм закон распред с параметрами а и σ²,

т.е. N(a;σ²), то практически достов, что ее знач заключены в интервале (a -3σ;a + 3σ):

Асимметрия нормального распределения А=0;

эксцесс нормального распределения Е =0.

24. Функция Лапласа и ее связь с ф распределен нормальной случайной величины.

Ф распред случ велич Х, распределенной по норм закону, выражается Ч/з функцию Лапласа Ф(х) по формуле

Где

Отметим свойства функции Ф(x):

1. Функция Ф(x) является нечетной, т.е. Ф(-x) = -Ф(x)

2. Функция Ф(x)–монотонно возрастающая при

положительных значениях x , причем при

x+.,Ф(x)1.

3. Практически можно считать, что уже при x > 4 Ф(x) ≈1.

25. Моменты случайных величин. Ассиметрия и эксцесс.

С реди числовых хар-к СВ особое значение имеют моменты–начальные и центральн.

Н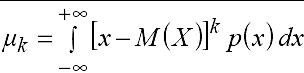 ачальн теор момент ряда k непрер случ велич Х опред-ся равенством

Ц ентральный теоретич момент порядка k непрерыв случ величины Х опред-ся равенством .

Матем ожидание М(Х), или первый начальный момент, харак-ет среднее значение распределения случ величины Х; второй централ момент или дисперсия D(X) – степень рассеяния распределения Х относительно М(Х).

Т ретий централ момент служит для харак-ки ассиметрии распред. Велич наз-ся коэф-том ассиметрии случайной величины. А=0, если распределение симм относ мат ожид.Четвертый центр момент характ-ет крутость распределения. Эксцессои случайной величины наз-ся число .

Число 3 вычитается из соотношения

так как для наиболее часто встреч норм распределения, отнош =3. Кривые, более островершинные, чем норм, облад

положит эксцессом,более плосковершин отриц эксцес

26. Неравенство Маркова.

27. Неравенства Чебышева. Следствия.

28. Теорема Чебышева и ее следствия.

29. Теорема Бернулли. Значение закона больших чисел.

Частость соб в n повторн незав испыт, в кажд из кот оно мож произ с одной и той же вероятн p, при неогран увелич числа n сходится по вероятности к вероятности p этого соб в отд испыт:

Или

Доказательство.

Введем случайные величины Х1, Х2, …, Хn, где Xi– число появлен А в i-м опыте.При этом Xi могут приним только два значения: 1(с

вероятностью р) и 0 (с вер q =1–p). Кроме того, рассматриваемые случ велич попарно независ и их дисперсии равномерно огранич

( D(Xi) =pq, p+q=1, откуда pq ≤¼). След, к ним мож прим теорему Чебышева при Mi = p