3.Комбинаторика – раздел математики, в к-ом изуч-ся вопросы о том, сколько различных подмножеств, обладающих заданными свойствами, можно выбрать из данного множества.
Осн.правила комбинаторики:
Правило суммы Если 2 действия взаимно искл. др. друга,причем одно из них м. выполнить m способами, а др-ое – n способами, то выполнить одно м. N=n + m способами
Правило умножения все k действий вместе могут быть
выполнены N= n1 n2 n3 nk способами
Перестановкой из n элементов-любой упорядоченный набор этих элементов.
Pn = n(n – 1)(n – 2)...321=n! (1!=1; 0!=1)
Размещениями из n элементов по k элементов - упорядоченные подмножества, состоящие из k эл-ов множества An.(Упорядоченное множество элементов-для к-го установлен порядок расположения элементов.)
Одно размещение из n эл-ов по k элементов м. отличаться от другого как набором эл-ов, так и порядком их расположения.
A kn =n!/(n-k)!
С
пособ
выбора,
приводящий
к перестановкам и размещениям называют
еще выборкой
без возвращений.
Число размещений с повторениями равно A kn = n k
Сочетаниями из n элементов по k элементов - подмножества, сост. из k элементов множества An. Одно сочетание от другого отлич. только составом выбран. элементов (но не порядком их расположения, как у размещений).сочетание C kn=n!/(n-k)!k!
Св-во числа сочетаний C mn= C m-nn
Сочетания с повторениями
C mn= C mn+m-1 =(n+m-1)!/(n-1)!m!
В сочетаниях с повторениями m может быть и больше n
4,5,6Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р (А + В) = Р (А) +Р (В) – Р (АВ).
Теорема сложения вероятностей несовместных событий. Если события А и В несовместны (т.е. k = 0), следовательно p(A+ B) = p(A) + p(B). Вер-ость появл. одного из двух несовм. событий, безразлично какого, равна сумме вероятностей этих событий. Следствие:Сумма вероятностей противоположных
с
обытий
равна 1.
P(A)+P(A)=1
Теорема умножения вероятностей. Вероятность совместного наступления двух событий равна произвед. вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
P( A× B) = P( A)× PA(B) .
В частности для независимых событий
P( A× B) = P( A)× P(B) ,т.е.вероятность совместного наступления двух независ. событий равна произведению вероятностей
этих событий.
Условная вероятность соб. А-вероятность соб. А, вычисленная при усл., что произошло событие В. Условная вероятность события А при усл., что событие В произошло обозначается индексами P(A/B) или PB (A). условная вероятность события А при усл.,что произошло событие В с P(B)0, опред. формулой
p(A/B)=k/m=p(AB)/p(B)
Свойства условных вероятностей
(аналогичны свойствам безусловной вероятности):
1) PB () =1; 2)PB () = 0; 3) 0PB (A)1; 4) если AC , то
P B (A) PB (С); 5) PB (A)=1 – PB (A)
Событие А называется независимым от
события В (с P(B)0), если PB (A) = P(A), т.е.
вероятность наступления события А не зависит от того,
произошло событие В или нет. Из опред. независимости непосредственно следует, что p(AB) = p(A) × p(B) для случая А и В – независимы.
Замечание.
В частности,если все n событий имеют одинак. вероятность, равную р, то вероятность появления хотя бы одного из этих событий P(A) 1 – (1–p)n
7
.Формула
полной вероятности.
Пусть
события Hi
,
i
=1,n
образуют
полную группу событий (P(Hi
)
> 0)
и
событие А может произойти с одним и
только с одним из этих событий.
Тогда
вероятность события А равна
P(A)=
(1)
В ф. (1)были заранее, до опыта, известны вероятности p(Hi) гипотез (до опытные вероятности назыв. еще априорными (из греческого)). Но чаще встреч. встречается, что что после опыта становится известной информация о его результатах.
Новые вероятности гипотез даются формулой Байеса
доказательство: по определению условной вероятности
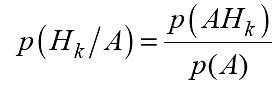
по
формуле умножения вероятностей
Тогда
Ф ормула Байеса. Если событие А произошло, то условные вероятности (апостериорные) гипотез Hi , (i =1,n) вычисляются по формуле, которая носит название формулы Байеса. где Р (А) – вероятность события А, вычисленная по формуле полной вероятности.