11.Ф-я распред-я случ велич. График

До сих пор в кач-ве исчерпыв описания ДСВ мы рассматр ее закон распред,представл собой ряд распред.Такое описание случ велич X не единств,не универс.Оно не применимо для непреp случ велич, 1.нельзя перечислить все бескон несчетное множ-во ее знач; 2.вероятн кажд отд взятого знач НепрСВ равны 0.

И дискр и непрер случ велич мож б задана функцией распред.

Функцией распределения случайной величины Х назыв ф F(x), выражающая для кажд х вер-ть , что случ велич Х примет знач меньшее х: F(x) = P(X < x)

Эта ф кажд действит числу x ставит в соответствие др действит число F(x) x F(x) = P(X < x)

Если знач случ велич– точки на числ оси, то геометр-ки ф распр интерпретир как вер, что случ велич Х попад левее заданн точк х. Пример 4. Найдем F(x) для , где ряд распр имеет вид:

x 0 1 2

p 0,12 0,46 0,42

Т огда, напр для 1<x≤2 F(x)=P(X=0)+P(x=1)=0,12+ 0,46=0,58.

График функции распределения

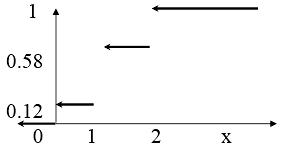Имеет ступенчатый вид

F (x) обладает свойствами:

1. Ф распр случ велич неотриц ф, заключ м/ду 0 и 1;0≤F(x)≤1.

2. Ф распр неубыв ф на всей оси. F(x2)=P(X<x2)=P((X<x1)+ (x1≤X<x2))=P(X<x1)+P(x1≤X<x2)=F(x1)+P(x1≤X<x2).

Т .к. P(x1≤X<x2)≥0 , то F(x2 )≥F(x1 ).

3. F(x)в x0 непрер слева, т.е.

4. На минус бесконечности ф распр =0, на плюс беск =1, т.е.

5. Вероятность попадания случайной величины в

интервал [x1,x2) равна приращению ее ф распр на этом интерв, P(x1≤X<x2)=F(x2)-F(x1).

6 . P(X≥x) =1- F(x)

7. Ф распр для дискр случ вел имеет вид

12. Мат ожид ДискрСлучВелич и его св-ва

Математическое ожидание М (Х)

Пусть случ велич Х может принимать только значения x1, x2 ,…, xn , вероятности которых соотв равны p1, p2 ,…, pn .Тогда мат ожид М (Х) случ велич Х опред-ся равенством

Из определения следует, что математическое ожидание дискр случ велич есть неслучайная (пост) велич.

Свойства математического ожидания

1. Математическое ожидание постоянной величины

равно самой постоянной: M(C) = C .

2. Пост множитель можно выносить за знак

математического ожидания: M(CX) = CM(X).

3. Мат ожидание алгебраической суммы

конечного числа случ величин равно алгебр сумме их мат ожид: M(X ± Y ) = M(X ) ± M(Y ).

4. Мат ожид произведения конечного числа незав случ величин равно произвед их мат ожиданий: M(XY ) = M(X )M(Y )

5. Мат ожид отклонения случ велич от ее мат ожид=0 M(X - M(X )) = 0.

M(X -M(X )) = M(X ) -M(M(X )) = M(X ) -M(X) = 0

13. Дисперс ДискрСВ, св-ва. Средн квадратич откл

На практике часто требуется оценить рассеяние возм знач случ велич вокруг ее ср знач.

Дисперсией D(X ) случайной величины Х называется мат ожидание квадрата ее отклонения от ее мат ожидания: D(X ) = M[X -M(X )]2 .

Дисперсия – это мера рассеяния случайной величины

около ее математического ожидания.

Е сли Х – дискретная случайная величина, то дисперсию вычисляют по следующим формулам

, (где а = М(Х));

Или D(X ) = M(X 2 )- (M(X ))2.

Доказательство. Используя то, что М(Х) –пост велич, и св-ва мат ожидания, преобразуем формулу к виду:

D(X) = M(X – M(X))² = M(X² - 2X·M(X) + M²(X)) = M(X²) –

2M(X)·M(X) + M²(X) = M(X²) – 2M²(X) + M²(X) =M(X²)-M²(X), что и требовалось доказать.

Свойства дисперсии случайной величины

1. Дисперсия постоянной величины =0: D(C) = 0 .

2. Постоянный множитель можно выносить за знак

дисперсии, возводя его в квадрат: D(CX ) = C²D(X ).

3. Дисперсия суммы двух незав случ величин равна сумме дисперсий этих величин: D(X + Y ) = D(X ) + D(Y ).

4. Дисперсия разности двух незав случ величин равна сумме их дисперсий: D (X – Y) = D (X) + D(Y).

С редним квадратическим отклонением σ случайной величины Х называется арифметич значение корня квадратного из ее дисперсии:

14.Биномиальный закон распределения

Если вер появл события А в каждом испытании пост и равна р, то число появлений события А – дискр случайная величина Х,принимающая значения 0,1,2,…, m, , n … с вероятностями

Д ругими словами, ряд распределения бином закона имеет вид:

Очевидно, что так как это есть сумма всех

членов разлож бинома

Ньютона(отсюда назв закона)

Мат ожид и дисперсия случ велич Х, распределенной по бином закону,вычисл соотв по формулам: M(X ) = np, D(X ) = npq

Доказательство. СВ X –число m наступлений события A в n незав испытаниях–можн предст в виде суммы n незав величин

каждая из кот имеет

о дин и тот же закон распред:

СВ Xk , кот называют индикат соб A, выраж число наступлений

соб A в k -м испытании k =1,2,...,n, т.е. при наступл события A Xk =1 с вероятностью p, при ненаступлении A Xk = 0 с вероятностью q .Числовые хар-ки индикатора события A :

M(Xk )= x1p1 + x2 p2 =1∙ p + 0∙q = p

Т аким образом, мат ожид и дисперсия рассматриваемой СВ X :

При нахожд дисперс суммы СВ учтена их незав. Теорема доказана

15. Закон Пуассона

Дискр велич X имеет закон распр Пуассона, если она принимает значения 0, 1, 2, , m,... (счетное множество значений) с вер-ми

где λ– некоторая полож велич,

называемая параметром закона

Пуассона.

Ряд распределения закона Пуассона имеет вид:

Определение закона Пуассона корректно, так как сумма

в сех вероятностей равна 1:

(разложение в ряд Тейлора функции eх при x =λ ).

Мат ожидание и дисперсия случ величины Х, распределенной по зак Пуассона,вычисл соотв по формулам: M(X)=λ D(X)=λ

Д -во

Д исперсию найдем по формуле

Теперь D(X) = M(X²) - (M(X))² =λ²+λ-λ²=λ , ч.т.д.

Сумма двух незав СВ,подчин распред Пуассона с параметрами

Λ1 и λ2, также имеет распред Пуассона с параметром λ1 +λ2 .

Замечание. Формул Пуас выраж бином распред при бол числе опыт и малой вер событ. Поэт зак Пуас назыв законом редк явл.

Зак Пуас подчин число α-частиц, достиг в теч времени t некот участка пространства,число клеток с измен под действием

рентгеновского излучения хромосомами, число

ошибочных телефонных вызовов в течение суток и т.д.

17. Непрерывные случ величины. Плотность вероятности

СВ Х называется непрер, если ее ф распред F(x) непрер в любой точке и дифференц всюду, кроме отдельных точек.

Примеры непрер СВ: диаметр детали,кот токарь обтачивает до заданного размера,рост человека, дальность полета снаряда и др.

Теорема. Вер-ть любого отдельно взятого знач непрерывной случайной величины равна 0: P(X = x1)=0.

Д оказательство. Используя свойство непрерывности F(x) имеем

Следствие.

Е сли Х – непрер СВ, то вер попадания СВ в интервал (x1,x2) не зависит от того, явл этот интерв открытым или закрытым, т.е.

Для непрер случайной величины P(x1 <X< x2 ) = F(x2 )- F(x1).

Задание непрер СВ с пом ф распред не явл единств возм. Для непрер СВ сущ неотриц ф p(x), удовлетвор при люб x равенству

Плотностью вер-ти (плотностью распред или просто плотн) р (х) непрер сл величины Х назыв произв ее ф распред: p(x)=F’(x)

Плотность вероятности р(х), как и ф распред F(х), явл одной из форм зак распред, но в отлич от ф распред она сущ только для непрерывных случайных величин.

Свойства плотности вер непрерывной случайной величины:

1 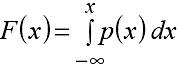. p(x)≥0;

2. Р(а≤Х≤ b)= 3.

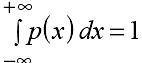
4.

Геом св-ва плотн вер означ, что ее график – кривая распред– лежит не ниже оси абсцисс, и полная площадь фигуры, огранич кривой распределения и осью абсцисс, равна единице.

18. Мат ожид и дисперсия непрер случ величины

М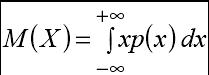 ат ожидание непрер СВ Х, возм знач кот принадл всей оси Ох, величина где р(х) – плотность

распределения случайной

величины.

П редполаг, что интеграл сходится абсолютно. В частности, если все возможные значения принадлеж интервалу (a;b), то

Дисперсия непрерывной СВ Х,возможные значения которые принадлежат всей оси Ох, определяется равенством

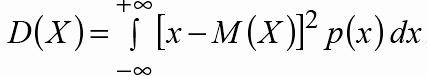или равносильным

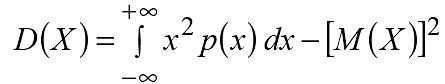
В частности, если все возм значения Х принадлежат (a;b), то

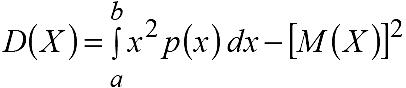Или

Все свойства мат ожидания и дисперсии для дискр СВ справедливы и для непрер величин.

Мат ожид 1. M(C) = C; 2. M(CX) = CM(X);

3. M(X±Y)= M(X)± M(Y) 4. M(XY)=M(X)M(Y);

5. Мат ожид отклонения случ велич от ее мат ожид=0 M(X-M(X))=M(X)-M(M(X))= M(X)-M(X) = 0

Дисперсия 1. D(Const)= 0 2. пост множ. D(CX)=C²D(X) 3. D(X+ Y)= D(X) + D(Y)

4. D (X – Y) = D (X) + D(Y)

Ср квадратическое отклонение непрерывной СВ

19. Равномерный закон распределения

Н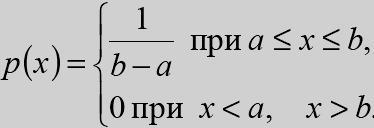 епрерывная случайная величина Х имеет равномерн закон распред на отрезке [a,b], если ее плотность

вероятности р(х) пост на этом отрезке и равна 0 вне его

Ф ункция распределения случайной величины Х,

распределенной по равномерному закону

20. Показательный закон распределения

Н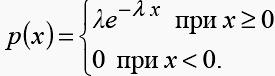 епр случайная величина Х имеет показательный (экспоненциальный) закон распред с параметром λ, если ее плотность вер имеет вид

Д ля случ величины, распределенной по показат зак

Д оказательство

Вер-ть попад в интервал (a;b) непрер случ велич Х, распред по

показ закону:

Замечание. Показат закон распреде вер встреч во мног задачах, связ с простейшим потоком событий. Под потоком соб поним послед-ть соб, наступ одно за другим в случайные моменты. Например, поток вызовов на телефонной станции.