Метод союзної (приєднаної) матриці

Нехай для даної неособливої матриці А потрібно знайти обернену матрицю А^-1.

Складемо для матриці А так звану союзну (приєднану) матрицю :

,

де – алгебраїчні доповнення відповідних елементів матриці А.

Обернена матриця А^-1 знаходиться за формулою:

.

Зразок виконання завдання

Завдання: Обернути матрицю А методом союзної (приєднаної) матриці:

.

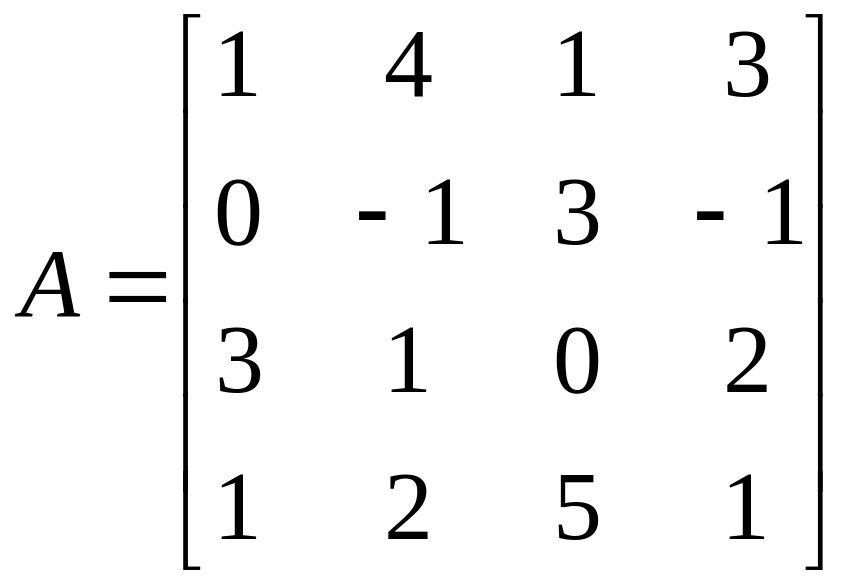Розв’язання:

Знаходимо визначник матриці А:

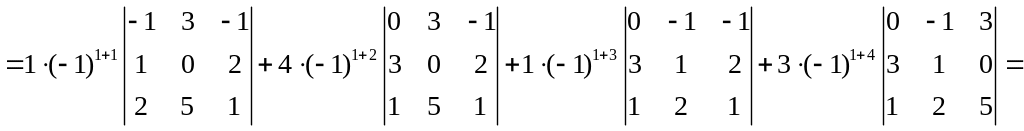
Матриця не вироджена. Отже, обернена існує.

Знаходимо алгебраїчні доповнення елементів матриці А:

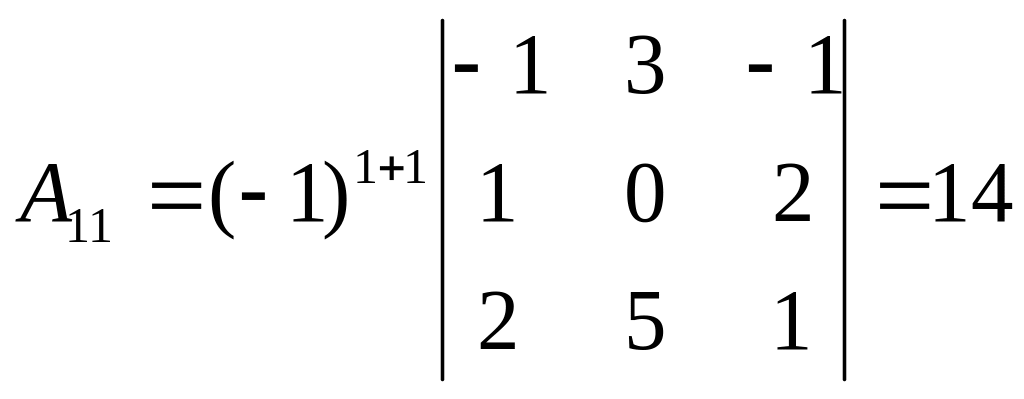, A₂₁ =22, A₃₁ = -2, A₄₁ = -16,

A₁₂ = 18, A₂₂ = 34, A₃₂ = 2, A₄₂ = -24,

A₁₃ =-4, A₂₃ = -8, A₃₃ = 0, A₄₃ = 4,

A₁₄ = -30, A₂₄ = -50, A₃₄ = -2, A₄₄ = 36.

Складаємо союзну (приєднану) матрицю:

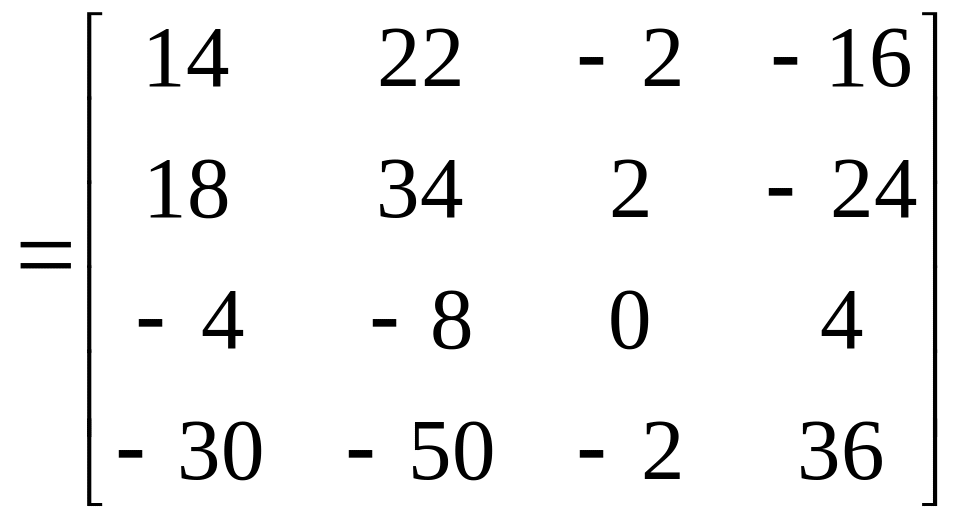
Знаходимо обернену матрицю:

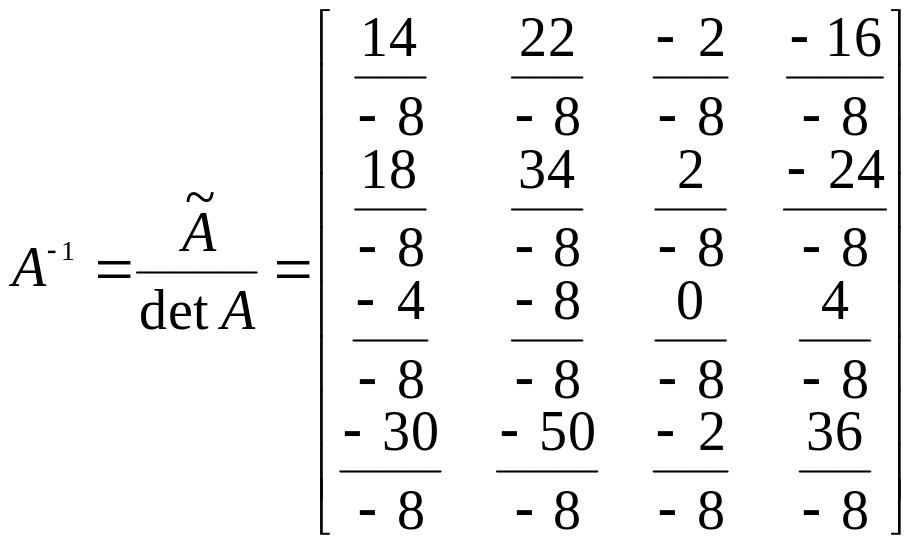
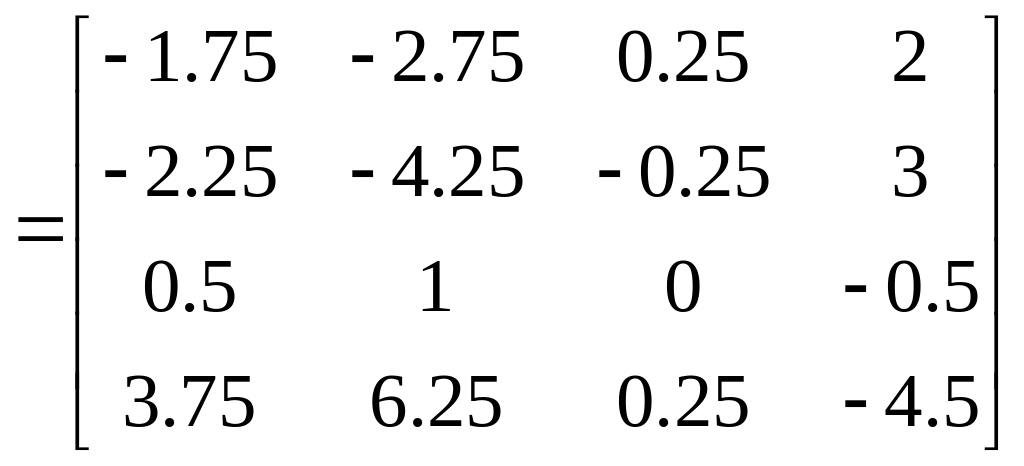
Виконуємо перевірку:

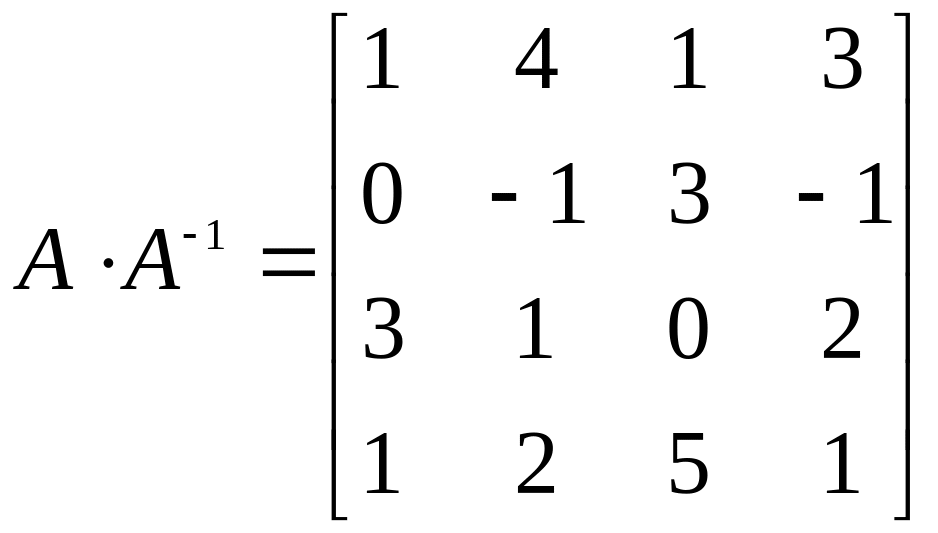
Відповідь:

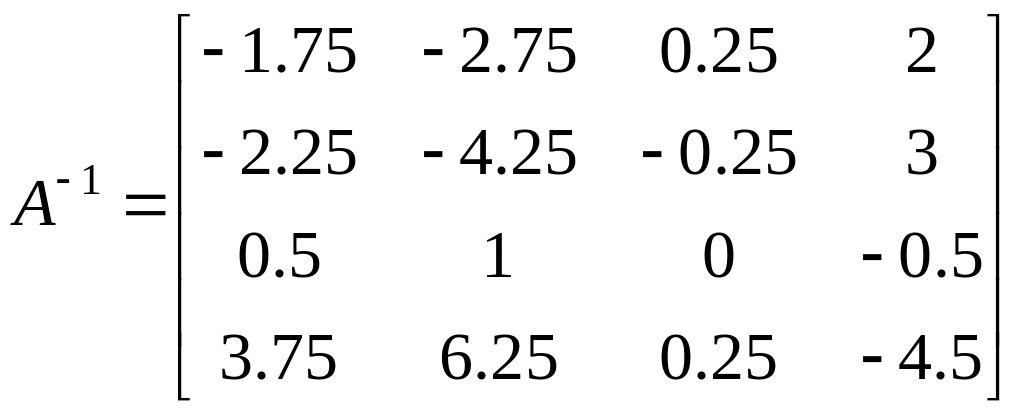
Приклад програми

// Обернути матрицю А методом союзної (приєднаної) матриці

#include <iostream.h>

#include <iomanip.h>

#include <conio.h>

#include <math.h>

int a[4][4]={{1,4,1,3},{0,-1,3,-1},{3,1,0,2},{1,2,5,1}};

int i,j;

float b[4][4],A[4][4];

int Det3(int x[3][3])

{

return x[0][0]*x[1][1]*x[2][2]+x[1][0]*x[2][1]*x[0][2]+x[0][1]*x[1][2]*x[2][0] -x[0][2]*x[1][1]*x[2][0]-x[2][1]*x[1][2]*x[0][0]-x[0][1]*x[1][0]*x[2][2];

}

int Minor(int X[4][4],int x,int y)

{

int m[3][3],i,j,i1,j1;

i=-1;

for (i1=0;i1<4;i1++)

{

j=-1;

if (i1!=x)

i++;

for (j1=0;j1<4;j1++)

if (i1!=x && j1!=y)

{

j++;

m[i][j]=X[i1][j1];

}

}

return Det3(m);

}

int Det4(int X[4][4])

{

int rez=0;

for (j=0;j<4;j++)

rez+=pow(-1,j)*X[0][j]*Minor(X,0,j);

return rez;

}

void main()

{

clrscr();

cout<<"Nahozhdenie obratnoy matrici pri pomoshi coyuznoy matrici";

cout<<endl<<"Zadayte matricu A:"<<endl;

for (i=0;i<4;i++)

for (j=0;j<4;j++)

{

cout<<"a["<<i+1<<","<<j+1<<"]= ";

cin>>a[i][j];

}

clrscr();

cout<<"Nahozhdenie obratnoy matrici pri pomoshi coyuznoy matrici";

cout<<endl<<"Matrica A (ishodnaya):"<<endl;

for (i=0;i<4;i++)

{

for (j=0;j<4;j++)

cout<<setw(5)<<a[i][j];

cout<<endl;

}

cout<<endl;

for (i=0;i<4;i++)

for (j=0;j<4;j++)

b[j][i]=pow(-1,i+j+2)*Minor(a,i,j);

int det=Det4(a);

cout<<"Opredelitel' Det(A)= "<<det<<endl;

cout<<"Soyuznaya matrica B:"<<endl;

for (i=0;i<4;i++)

{

for (j=0;j<4;j++)

cout<<setw(5)<<b[i][j];

cout<<endl;

}

for (i=0;i<4;i++)

for (j=0;j<4;j++)

A[i][j]=b[i][j]/det;

cout<<endl;

cout<<"Obratnaya matrica R:"<<endl;

for (i=0;i<4;i++)

{

for (j=0;j<4;j++)

cout<<setw(12)<<A[i][j];

cout<<endl;

}

getch();

}