4. Реализационные характеристики фильтра

Определим реализационные характеристики цифрового фильтра по структурным схемам. Реализационные характеристики определяют сложность аппаратной реализации, и моделирования фильтра в реальном масштабе времени.

- число ячеек оперативной памяти, необходимое для реализации фильтра. Оно равно числу элементов задержки в структурной схеме.

- число ячеек постоянной памяти, необходимое для реализации фильтра. Оно равно числу различных постоянных множителей.

- число операций умножения, которое должно быть выполнено за время для получения одного отсчета выходного сигнала. Оно равно числу множительных устройств.

- число операций сложения. Оно равно суммарному числу входов сумматоров, минус число сумматоров.

Реализационные характеристики фильтра при построении прямым способом: , , ,

Реализационные характеристики фильтра при построении каноническим способом: , , , .

5. Синтез цифрового фильтра в системе программирования matlab

Произведем проверку коэффициентов передаточной функции цифрового фильтра полученных после выполнения первого и второго пунктов задания.

Для вычисления коэффициентов передаточной функции ФВЧ Баттерворта порядка n, с частотой среза служит команда: [b, a] = butter(n,W_c). Частота задается в единицах нормированной частоты , т.е. значение этой частоты находится в интервале [0,1], где 1 соответствует частоте Найквиста. Частота Найквиста равна половине частоты дискретизации.

М-сценарий:

close all, clear, clc

n = 3; fc = 100; fd = 5000;

Wn = 2*fc/fd;

[a, b] = butter(n,Wn)

Получаем:

Wn =

0.0400

a =

1.0e-003 *

0.2196 0.6588 0.6588 0.2196

b =

1.0000 -2.7488 2.5282 -0.7776

Таблица 1. Коэффициенты фильтра

Рассчитанные коэффициенты		Коэффициенты, полученные в MATLAB			Погрешность расчёта
а	b		а	b		а	b
0,2187	1		0,2196	1		0,0009	0
0,6561	-2,7492		0,6588	-2,7488		0,0027	0,0004
0,6561	2,5289		0,6588	2,5282		0,0027	0,0007
0,2187	-0,7779		0,2196	-0,7776		0,0009	0,0003

6. Частотные характеристики цифрового фильтра

Группа функций freqz выполняет расчет частотной характеристики по передаточной функции цифрового фильтра, заданной векторами коэффициентов знаменателя и числителя .

М-сценарий:

close all, clear, clc

n = 3; fc = 100; fd = 5000;

% w = 2*pi*fc

Wn = 2*fc/fd;

[a, b] = butter(n, Wn)

freqz(a, b)

Получившиеся АЧХ и ФЧХ изображены на рисунке 3.

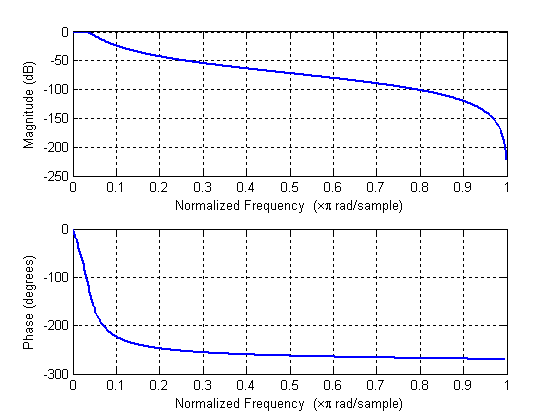
Рисунок 3. АЧХ и ФЧХ цифрового фильтра нижних частот