2. Расчет передаточной функции цифрового фильтра

Передаточную функцию цифрового фильтра получим отображением комплексной S-плоскости в P-плоскость (денормирование частоты).

Денормируем частоту в аналоговой области. Заменим аргумент передаточной функции функцией . Для этого воспользуемся справочными данными [1]: .

В результате получим функцию дробно-рационального вида

(2.1)

Коэффициенты передаточной функции (2.1) возьмем из справочных данных [1]:

После подстановки табличных значений в формулу (2.1) получим передато чную характеристику :

(2.2)

где - частота среза [рад/с].

Произведем билинейное преобразование:

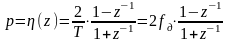, (2.3)

получим передаточную характеристику в виде:

(2.4)

Коэффициенты передаточной функции (2.4) возьмем из справочных данных [1] и рассчитаем их:

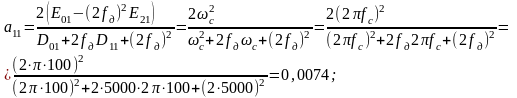
Подставив полученные коэффициенты в передаточную характеристику вида (2.4) получим:

3. Структурные схемы фильтра

Для рекурсивных фильтров соотношение между входной последовательностью и откликом может быть записано в виде:

, (3.1)

то есть текущий отсчет отклика определяется не только текущим и предшествующим значениями входной последовательности, но и предшествующими отсчетами отклика.

Как уже отмечалось, z-преобразование, соответствующее цифровому фильтру, можно выразить в виде дробно-рационального полинома от переменной z^-1, т.е.

, (3.2)

Приведя равенство к общему знаменателю, получим разностное уравнение:

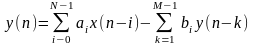. (3.3)

Задержка отсчетов в передаточной функции отображается следующем образом: , . Свободный член знаменателя соответствует реакции .

Уравнение (3.3) реализует прямую форму. В ней для преобразования цепей, соответствующих числителю и знаменателю формулы (3.2), используются раздельные элементы задержки.

По передаточной функции цифрового фильтра (2.5) построим структурную схему его реализации прямым способом. Для построения структурной схемы по известной передаточной функции получим уравнение в конечных разностях. Во-первых, запишем передаточную функцию:

(3.6)

Во-вторых, выразим из данного соотношения :

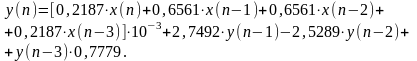(3.7)

На основании формулы (3.7) построим структурную схему рекурсивного фильтра рисунок 1. Коэффициенты передаточной функции приведены в таблице 1.

a2

a1

a3

b2

b3

b4

z^-1

z^-1

z^-1

z^-1

z^-1

z^-1

Σ

Рисунок 1. Прямая форма построения ЦФ

Если записать формулу (3.2) в ином виде:

, (3.8)

то можно получить другую структуру цифрового фильтра. Такой фильтр состоит из двух последовательно соединенных фильтров с коэффициентами передачи соответственно 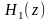и . Первый из фильтров имеет только полюсы, а второй – только нули.

Запишем передаточную функцию следующим образом

; (3.9)

рекурсивная часть фильтра,

; (3.10)

нерекурсивная часть фильтра.

Тогда получим пару разностных уравнений:

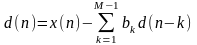; (3.11)

. (3.12)

Для построения структурной схемы каноническим методом запишем передаточную функцию (2.5) следующим образом:

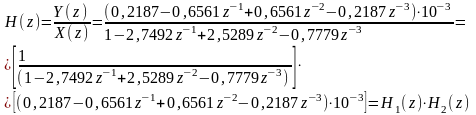(3.13)

В этом случае разностные уравнения (3.9) и (3.10) примут вид:

(3.14)

(3.15)

Поскольку в цепях, соответствующих и , сигнал задерживается одинаковое количество отсчетов, то для построения фильтра

достаточно использовать один набор элементов задержки. Такую структуру называют канонической формой, так как в ней используется минимальное количество элементов.

По уравнениям (3.14) и (3.15) построим структурную схему фильтра, изображенную на рисунке 2.

Σ

X

z^-1

z^-1

z^-1

Σ

a1

a2

a3

b1

b4

b3

b2

Y

Рисунок 2. Каноническая форма построения ЦФ

При использовании канонического способа построения структурной схемы в ее составе всегда будет два сумматора, причем выходной сигнал первого из них всегда будет равен функции .