Применение критерия предельной пластичности для острых концентраторов

Развитие линейной механики разрушения было вызвано тем, что в рамках классической механики материалов (КMМ) не удавалось описать поведение конструкций с острыми концентраторами напряжения на основе характеристик материала, полученных при испытании образцов с концентраторами ограниченной остроты. Критерий предельной пластичности действует в рамках КММ, поэтому при описании на его основе процессов страгивания трещин от острых концентраторов и процессов роста трещин также встречаются определенные трудности, которые отсутствуют при моделировании разрушения в условиях низких градиентов полей НДС.

Во-первых, необходима высокая точность моделирования НДС вблизи вершины концентратора. При моделировании МКЭ это требует достаточно мелкой сетки (с минимальным размером элемента порядка 1 мкм), полного комплекта механических характеристик материала, включая диаграммы упрочнения и предельной пластичности, правильного задания граничных условий и учета при расчете НДС как физической нелинейности (текучести) так и геометрической (больших деформаций в зоне концентратора). Весь процесс нагружения (в особенности, циклического) необходимо разбить на такие шаги, в пределах каждого из которых траекторию деформаций можно считать линейной. При нагружении, близком к простому, возможно применение крупных шагов без потери точности.

Во-вторых, необходимо моделировать процесс развития разрушения, даже если предельным состоянием является страгивание трещины от концентратора. Расчет, даже при учете геометрической нелинейности, дает вблизи острого концентратора деформации, многократно превышающие предельную пластичность материала. При этом измельчение конечных элементов не обеспечивает получения однозначного решения. В качестве решения этой проблемы было предложено применять критерий предельной пластичности и считать разрушенными (не существующими) те конечные элементы, в которых уровень поврежденности найденный по формуле (40), достигает 100%. При определенных условиях начало разрушения от вершины острого концентратора приводит к его притуплению и торможению страгивания трещины. Для получения этого эффекта на модели соотношение размеров элементов в зоне разрушения и шагов приращения нагрузки должно быть таким, чтобы на каждом шаге разрушалось более одного конечного элемента.

Эксперименты показывают, что влияние поврежденности на макроскопические параметры упругости материала начинается при деформации порядка 70% от предельной пластичности, что соответствует уровню поврежденности около 50%. При дальнейшей деформации материал ведет себя как пористое тело, т. е. становится сжимаемым. Его объемный модуль упругости снижается и, по мере роста поврежденности, стремится к 0. Снижение модуля сдвига происходит позднее, при поврежденности, близкой к 100%. Это явление приводит к снижению объемности НДС в поврежденной зоне и также тормозит страгивание и рост трещины.

Результаты применения разработанной методики для моделирования процесса испытаний на трехточечный изгиб призматического образца из стали 15Х2МФА с острым надрезом глубиной ℓ=35 мм представлены на рис. 60.

Использование диаграммы упрочнения стали 15Х2МФА (см. рис. 57) обеспечило хорошее совпадение с экспериментально полученной зависимостью раскрытия надреза от приложенного усилия, как в упругой области, так и на начальном участке упруго-пластических деформаций. Однако затем кривая 2, построенная без учета разрушения металла в концентраторе отклонилась вверх от экспериментальной кривой 1. Применение критерия предельной пластичности (см. рис. 58) обеспечило совпадение результата моделирования с экспериментом вплоть до полного разрушения образца (кривая 3 на рис. 60).

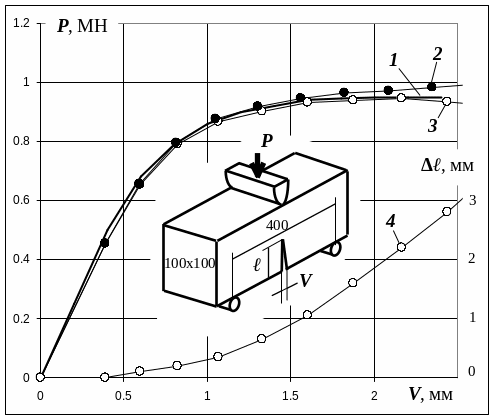
Рис. 60. Моделирование разрушения образца с боковым надрезом из 15Х2МФА: 1 - эксперимент, 2 – модель без учета разрушения, 3,4 – модель с учетом роста трещины (3 – сила, 4 - рост трещины)

Моделирование показало, что рост трещины начинается на ранней стадии нагружения (при раскрытии надреза около 0,5 мм), но не оказывает заметного влияния на взаимное перемещение половин образца при длине трещины менее 1 мм (при раскрытии надреза до 1,5 мм). Как и в эксперименте, рост трещины в модели происходил в плоскости исходного надреза. При длине трещины 2 мм рост нагрузки прекратился (уменьшение сечения компенсировало упрочнение его неразрушенной части). К моменту долома образца длина трещины достигла 3 мм.

Если чередовать шаги с приращением нагрузки и шаги «на месте» (при постоянной нагрузке), то можно оценить устойчивость (стабильность) процесса разрушения. При нестабильном разрушении рост трещины не затухает при отсутствии роста нагрузки, а продолжается с нарастающей скоростью и за счет изменения геометрии концентратора и перераспределения напряжений.