Критерий предельной пластичности

Критерий предельной пластичности является общепризнанным в теории обработки давлением для условий сложного напряженного состояния. Согласно теории пластического разрыхления В.В.Новожилова, на разрушение влияют два основных фактора:

1. Пластическая деформация непрерывно порождает дислокации и микродефекты, приводящие к разрыхлению, т. е. уменьшению плотности металла. Пластическая деформация происходит по механизму сдвига (рис. 52). В идеальном кристалле возможна большая деформация вдоль одной из плоскостей решетки без возникновения дислокаций. В реальном поликристаллическом теле на границе зерен возникает несовпадение плоскостей, в результате возникают микропоры. Их появление доказано измерениями плотности: она понижается в процессе пластических деформаций, даже под действием сжимающих напряжений.

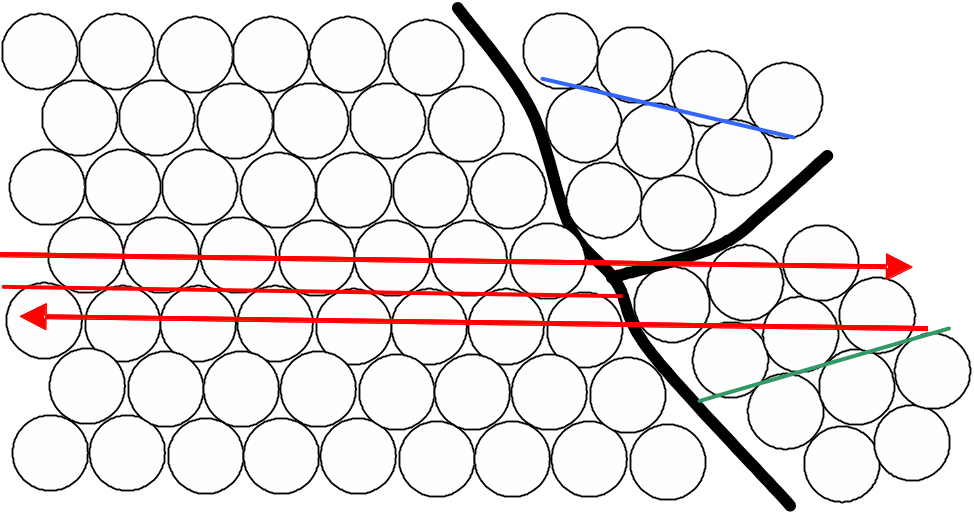
Рис. 52. Схема пластической деформации поликристаллического материала

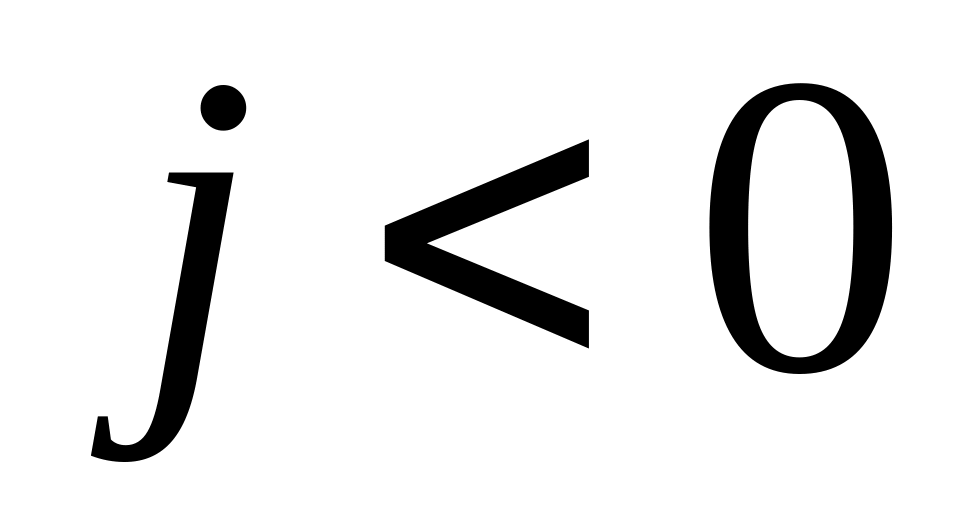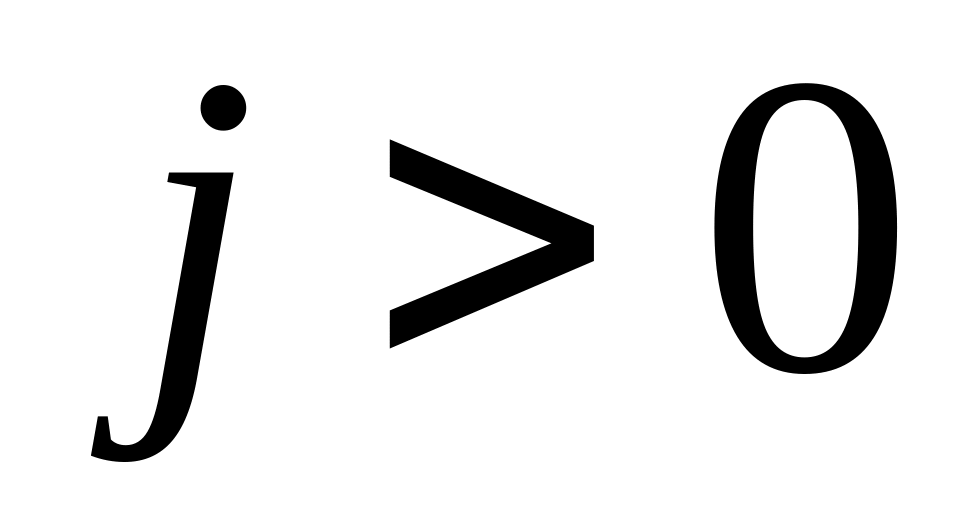2. от схемы напряженного состояния, важнейшим параметром которой является показатель объемности j, зависит развитие возникших дефектов: при сжатии дефекты закрываются, что приводит к росту пластичности; при растяжении дефекты раскрываются, а пластичность падает.

, (39)

где - гидростатическая составляющая тензора напряжения, - интенсивность напряжения. Предельная пластичность является характеристикой материала, аналогичной диаграмме упрочнения, и может быть представлена в виде зависимости .

При , когда все главные компоненты напряжения отрицательны, материал испытывает всестороннее сжатие, и образовавшаяся пора залечивается, стягиваясь в точку (рис. 53). При этом у некоторых материалов наблюдается неограниченная пластичность. Залечивание возможно и при одном положительном компоненте, вытягивающем пору в нить, поскольку 2 других компонента сжимающие. Даже один сжимающий компонент при может «расплющить» и залечить дефект. Если же все 3 компонента напряжения растягивающие, то образовавшиеся дефекты не залечиваются а растут, что приводит к вязкому разрушению (разрыву перемычек между выросшими порами).

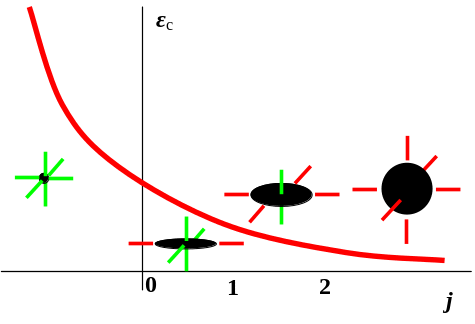
Рис. 53. Зависимость предельной пластичности от показателя объемности НДС

Для построения диаграммы предельной пластичности в области были использованы испытания образцов на растяжение в камере, наполненной жидкостью под давлением. Для оценки прочности и ресурса более важна область , в которой пластичность ниже. Для нее были использованы образцы с надрезами различной остроты.

На рис. 54 показаны результаты испытания на растяжение цилиндрических образцов с кольцевыми надрезами. На диаграммах отмечены точки начала пластических деформаций (B), образования шейки (N), а также зарождения трещины в шейке образца (K).

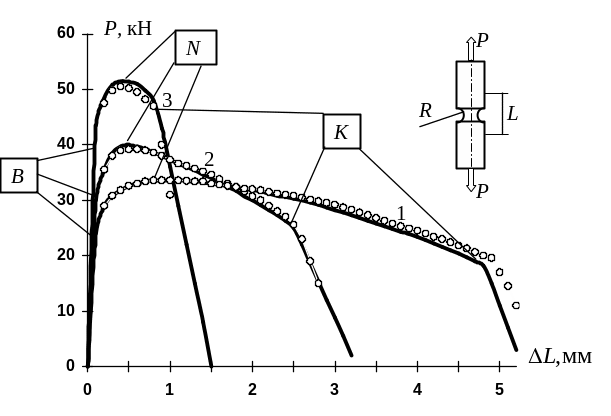
Рис. 54. Результаты испытаний гладкого цилиндрического образца (1) и образцов с надрезами радиусом R=10 мм (2) и R=2 мм (3) из стали 15Х2МФА. Линии – эксперимент, точки – расчет

Для получения таких диаграмм потребовалась специальная установка для жесткого нагружения, в которой параллельно образцу растягивались 2 упругих стержня (рис. 55). Обычно сразу после образования шейки происходит дорыв образца. Стержни брали на себя нагрузку и не давали захватам машины разлетаться в разные стороны даже после полного разрушения образца.

Критерий предельной пластичности был разработан и применялся для технологических задач обработки давлением, в условиях малых градиентов напряжений. В области острых концентраторов эти градиенты очень большие, поэтому потребовалась доработка критерия, чтобы его можно было применить для оценки ресурса сварных конструкций с дефектами.

Основным препятствием при разработке единой модели разрушения для вязкого и хрупкого разрушения от концентраторов различной остроты являлось обнаруживаемое в экспериментах различие критических уровней НДС для одного и того же материала. Этот результат привел в свое время к отказу от классической механики материалов и попыткам решения задачи средствами механики разрушения. Однако область применимости известных подходов механики разрушения также весьма ограничена.

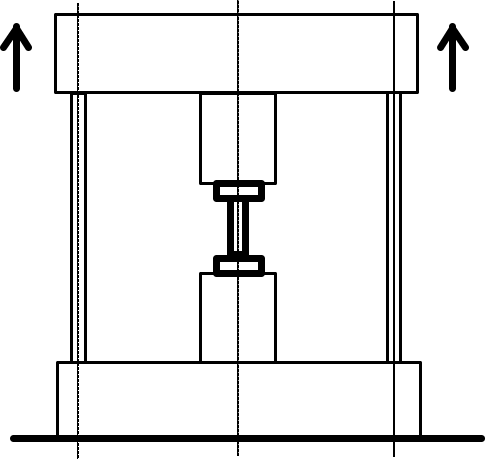
Рис. 55. Установка для жесткого нагружения

Возможно другое решение проблемы, более эффективное при расчете сварных конструкций. Для этого, кроме применения критерия предельной пластичности и модели накопления повреждений, необходимо принять следующие положения, позволяющие получить одинаковые критические значения критерия для всех условий разрушения. Эти положения составляют основу метода, который можно назвать прямым моделированием процесса разрушения.

1. Для того, чтобы при моделировании зон с различными градиентами НДС можно было использовать единые характеристики материала, необходимо повысить точность моделирования НДС, учесть физическую и геометрическую нелинейность у острого концентратора. Для решения этой задачи на кафедре сварки МГТУ им. Баумана был разработан специализированный программный комплекс “Сварка”.

2. Методика получения характеристик материала должна включать непрерывную запись регистрируемых параметров при испытаниях и моделирование на ЭВМ испытанных образцов. Показателем точности полученных характеристик материала является точность воспроизведения на модели параметров, записанных при испытании.

3. При моделировании процесса разрушения все зоны, в которых рассчитанные параметры НДС оказываются выше критических параметров моделируемого материала, следует считать разрушенными, а материал внутри этих зон не сплошным, а пористым (с пониженными механическими характеристиками) или не существующим (с характеристиками, близкими к нулю).

4. При выполнении первых трех условий можно считать критерий разрушения зависящим только от НДС и свойств материала в данной точке и не зависящим от состояния в соседних точках, градиентов и геометрических параметров концентратора.

Физическая достоверность третьего из выдвинутых положений требует дополнительной проверки, однако практическую ценность такого подхода в качестве основы модели можно считать доказанной, поскольку он позволил с высокой точностью воспроизвести на модели деформирование и разрушение как гладких образцов, так и образцов с различными надрезами и трещинами при растяжении и изгибе (на рис. 54 видно, что расчет достаточно точно воспроизводит в том числе и участок роста трещины в шейке образца после точки страгивания трещины K).

В частности, получено объяснение независимости прочности от остроты надреза, если радиус остроты меньше критического. Моделирование показало, что зона разрушения от острого надреза или трещины имеет малую глубину, то есть разрушение распространяется по внутренней поверхности трещины, приводит к притуплению трещины и тормозит увеличение ее глубины. Это связано с тем, что при ограниченных размерах пластической зоны пластическая деформация локализована у фронта исходной трещины и резко убывает по направлению вглубь металла. Обычно эта начальная фаза, на которой разрушение происходит, а трещина не растет, остается незамеченной в экспериментах.

При дальнейшем раскрытии трещины растет размер пластической зоны, а градиент убывания пластической деформации на продолжении трещины уменьшается. В этих условиях сильнее сказывается влияние различной объемности НДС на различных направлениях от фронта исходной трещины. Разрушение концентрируется в направлении наибольшей объемности (для трещины нормального отрыва это направление совпадает с продолжением исходной трещины), одновременно увеличивается протяженность зоны разрушения в глубину металла. Начиная с этого момента рост глубины трещины становится заметным и в экспериментах принимается за начало разрушения.

С другой стороны, углубление трещины может быть вызвано не только разделением частиц материала. Раскрытие трещины вызывает перед ее фронтом удлинение волокон, перпендикулярных к плоскости трещины. При этом происходит их поперечная утяжка, в результате поперечное сечение волокон перед фронтом трещины уменьшается, что приводит к ее углублению. Приповерхностный слой у дна трещины находится в условиях плоского напряженного состояния. К моменту достижения разрушающей деформации, если она имеет порядок 100%, поперечное сечение волокон сокращается вдвое. В этом случае половина убывания прочности волокон связана с их поперечной утяжкой перед разрывом и только половина - с их разрывом. Продвижение трещины за счет поперечной утяжки металла перед ее фронтом можно назвать локальной потерей пластической устойчивости.

Как показывает моделирование, рост трещины в глубину металла вызван совместным действием механизмов утяжки и разрыва волокон. Роль каждого из них зависит от пластичности материала на пути движения трещины. При малой пластичности основную часть потери прочности ослабленного сечения вызывает разрыв волокон, а при большой - их утяжка.

Прямой характер моделированию придает то, что рост трещины моделируется не на основе критерия, описывающего некоторую область, содержащую острый концентратор, что присуще всем критериям ЛМР, а на основе свойств, проявляемых материалом и в однородном НДС. В качестве такой характеристики нами выбрана предельная пластичность материала, являющаяся функцией показателя объемности напряженного состояния.

Деформационная характеристика материала, ее зависимость от температуры, скорости и других условий нагружения

Деформационная характеристика материала широко применяется в расчетах НДС конструкций, хотя до недавнего времени считалось, что для полного описания механических свойств материала достаточно указать его предел текучести , предел прочности и относительное удлинение , которые являются частными параметрами .

Основным новым элементом при переходе к моделированию процесса разрушения является разработка методики построения и применения характеристики предельной пластичности взамен критериев разрушения более узкого применения, таких как .

Как выяснилось из сопоставления результатов моделирования с экспериментами, методика построения также требует существенной доработки. Обычная методика построения сводится к обработке только начального участка машинной диаграммы испытания образцов на растяжение (до образования шейки), с последующей аппроксимацией результатов степенной функцией вида

. (40)

Далее эту функцию экстраполируют вплоть до точки разрушения. В некоторых случаях коэффициенты аппроксимации уточняют с учетом результатов обмера разрушенного образца. Однако такое уточнение затруднено тем, что распределение НДС после появление шейки становится неравномерным. Шейка может появиться на любом участке гладкой части образца, что затрудняет решение этой сравнительно простой задачи численными методами. До настоящего времени стандартная методика расчета НДС в шейке основана на аналитических решениях, которые получены с использованием весьма грубых допущений. Одной из причин несовершенства методики следует считать отсутствие практической потребности в точном моделировании НДС при больших деформациях. Ситуация меняется при переходе к моделированию разрушения металла.

Как показали испытания листового материала при двухосном растяжении, использование единой степенной аппроксимации для всего участка от площадки текучести до разрушения в принципе неверно. При двухосном растяжении сферической оболочки внутренним давлением образование местного утонения (“шейки”) сопровождается выпучиванием этого участка, уменьшением радиуса его кривизны и снижением мембранных напряжений. Это явление позволяет обеспечить устойчивость и равномерность деформаций на достаточно широком участке оболочки вдали от закреплений вплоть до разрушения и непосредственно регистрировать изменение показателя упрочнения n. У всех десяти испытанных марок стали было зафиксировано изменение показателя упрочнения, причем перед разрушением все они имели участок диаграммы с n = 0.

Повысить точность моделирования образцов на ЭВМ удалось как за счет совершенствования математической модели с учетом геометрической и физической нелинейности, так и за счет изменения конструкции образца. Большая длина гладкой части стандартных цилиндрических образцов (5 или 10 диаметров) нужна для более точного построения начальной части деформационной характеристики (до ). Чем длиннее образец, тем меньшую долю от его удлинения составляет удлинение шейки. Таким образом, для конструкционных материалов с высоким значением показателя упрочнения (n > 0,1) показывает относительное удлинение образца до образования шейки и не характеризует пластичность к моменту разрушения. Сокращение длины гладкой части образца до 2 - 2,5 диаметров обеспечивает образование шейки не в произвольном сечении, а всегда на середине длины, существенно облегчает изготовление и моделирование образца и повышает точность построения конечного участка деформационной характеристики. Разработанная в МГТУ методика построения основана на решении обратной задачи, то есть на подборе такой характеристики, которая обеспечивает полное совпадение результатов моделирования с машинной диаграммой, полученной усреднением результатов испытаний нескольких образцов, от начала нагружения до начала разрушения.

Порядок обработки «машинной» диаграммы испытаний (рис. 56):

1) Построить участок зависимости до образования шейки .

2) Первое приближение для зависимости на участке образования и развития шейки получить путем проведения прямой B'K' по касательной к кривой построенного участка .

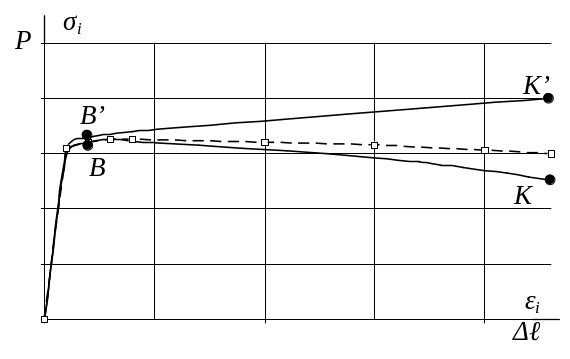
Рис. 56. Схема использования метода последовательных приближений (подбора) при построении зависимости

3) С использованием этой приближенной зависимости провести пробное пошаговое моделирование процесса нагружения гладкого образца методом конечных элементов и построить отдельные точки машинной диаграммы гладкого образца (штрих пунктирная линия на рис. 56).

4) С учетом погрешности ординат машинной диаграммы, полученных при пробном моделировании, внести поправки в значения ординат деформационной характеристики и повторением пунктов 3) и 4) обеспечить требуемую точность совпадения машинной диаграммы гладкого образца с расчетной, получаемой методом моделирования.

При отработке методики были использованы результаты испытаний образцов из двух марок стали 02Х10Н9МТ и 15Х2МФА, весьма тщательно проведенных А.А.Лебедевым на специальной установке, обеспечивающей постоянство скорости нагружения как до, так и после образования шейки на образце.

Моделирование подтвердило независимость деформационной характеристики от схемы напряженного состояния. Характеристика (рис. 57), подобранная для гладкого образца, позволила с высокой точностью воспроизвести и все диаграммы образцов с кольцевыми надрезами радиусом R = 2, 4, 10 и 20 мм. Погрешность не превышала 5% для стали 15Х2МФА и 1% для 02Х10Н9МТ. Дополнительной проверкой стало сопоставление с результатами обмера шейки образцов в момент образования трещины. Погрешность расчета диаметра шейки при соответствующих значениях нагрузки также не превышала 5% для стали 15Х2МФА и 1% для 02Х10Н9МТ.

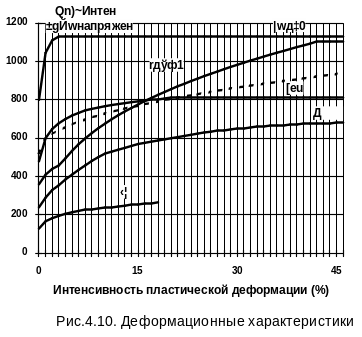
Рис. 57. Деформационные характеристики материалов

Из рис. 57 видно, что построенная таким способом диаграмма для стали 15Х2МФА близка к построенной по обычной методике (пунктир) на начальном участке, но расходится с ней после образования шейки. Моделирование результатов испытаний сталей 15Х2МФА и 02Х10Н9МТ, а также испытанной нами стали 20 показало, что на завершающем участке диаграммы при осевом растяжении, так же как при двухосном, показатель упрочнения n стремится к нулю.

Таким образом, разработанная методика обеспечивает высокую точность при одновременном снижении требований к образцам. Характеристика может быть построена по результатам испытаний как гладкого, так и образца с надрезом.

Дальнейшая обработка машинных диаграмм позволяет построить диаграмму пластичности. Методика А.А.Лебедева включала остановку испытаний на разных стадиях и разрезку образцов вдоль, что позволяло определить место возникновения трещины и соответствующую точку машинной диаграммы (К на рис. 54).

Как правило, разрушение начиналось от точки с максимальной объемностью НДС. Значения и j в этой точке модели, при нагрузке, соответствующей точке T машинной диаграммы, позволяют получить одну точку диаграммы пластичности. Вся диаграмма может быть построена на основе испытания серии образцов с различной остротой или глубиной надреза.

Порядок построения диаграммы пластичности:

1) По результатам моделирования НДС гладкого образца для шага нагружения, соответствующего точке K (начала роста трещины) на рис. 54 и 56, проанализировать распределения объемности НДС и пластической деформации в сечении шейки (рис. 58), установить зону сечения, где объемность максимальна и определить значение , вызывающее появление макротрещины в этой зоне. Таким образом получаем одну точку диаграмму пластичности.

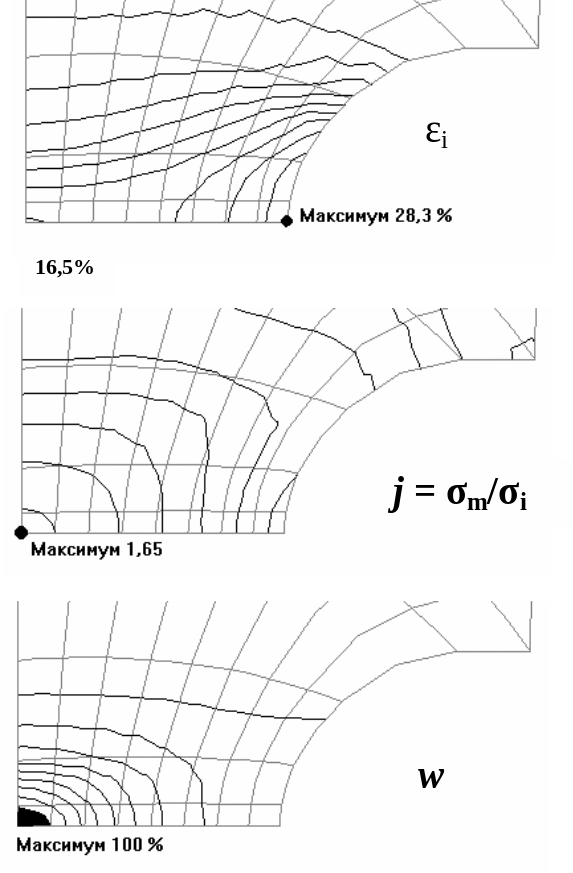
Рис. 59. Распределение интенсивности пластических деформаций ε_i, объемности напряженного состояния j и поврежденности w в шейке образца в начале разрушения

2) Повторить пункт 1) для каждого из образцов с кольцевыми проточками различных радиусов и по совокупности этих точек построить диаграмму пластичности.

В принципе j может быть любым, но для моделирования процесса разрушения наибольший интерес представляет участок диаграммы 0 < j < 3, то есть с преобладанием растяжения. Наибольший показатель объемности, который можно наблюдать перед вершиной трещины в упрочняющемся материале, составляет 2,5 - 3. Образцы с надрезами при растяжении имеют до образования трещины j от 0,33 до 2, в зависимости от радиуса надреза. Полученные диаграммы показаны на рис. 59.

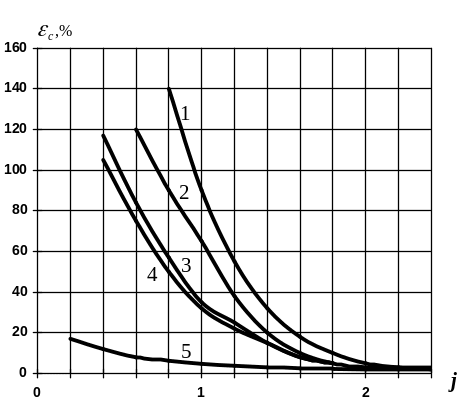
Рис. 59. Диаграммы предельной пластичности различных сплавов: 1 - сталь 02Х10Н9МТ, 2 - сталь 15Х2МФА, 3 – сталь Ст20, 4 – сталь 17ГС, 5 – магниево-литиевый сплав ИМВ-2

Для получения большей объемности можно привлечь результаты испытаний образцов с трещиной.