
- •Билет№3
- •Билет №4
- •Билет№5
- •Билет №6. Линейная функция и Степенная функция. Их графики
- •Билет№7. Градиент функции двух переменных и его свойства.
- •Билет №9.
- •Билет №10. Числовые последовательности и способы их задания. Примеры.
- •Билет №14.
- •Билет№15. Ограниченные последовательности. Теорема о существовании предела ограниченной последовательности. Число е.
- •Билет№ 16. Предел функции. Определение через окрестность. Графическая иллюстрация.
- •Билет№ 17. Предел функции. Определение через пределы последовательности. Доказать, что функция Дирихле ни в одной точке не имеет предела.
- •18 Билет Теорема о двух полицейских для функций. Первый замечательный пример ( с доказательством ). Пример.
- •Второй замечательный предел. Примеры.
- •Билет 23Односторонние пределы функции
- •Вопрос № 24 Понятие производной функции (1). Понятие секущей и касательной (2). Геометрический смысл производной (3).
- •Билет №27.
- •Билет №32. Производная обратной функции, производная арксинуса и арктангенса
- •Билет №33. Свойства функций, непрерывных на отрезке, теорема Ролля, теорема Лагранжа
- •Билет №34. Дифференциал и его геометрическое значение.
Билет №6. Линейная функция и Степенная функция. Их графики
Линейная функция — функция вида
![]() (для
функций одной переменной).
(для
функций одной переменной).
Основное свойство линейных функций: приращение функции пропорционально приращению аргумента.
![]() является тангенсом угла,
который образует прямая с положительным
направлением оси абсцисс.
является тангенсом угла,
который образует прямая с положительным
направлением оси абсцисс.
При
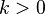 ,
прямая образует острый угол с осью абсцисс.
,
прямая образует острый угол с осью абсцисс.При
 ,
прямая образует тупой угол с осью абсцисс.
,
прямая образует тупой угол с осью абсцисс.При
 ,
прямая параллельна оси абсцисс.
,
прямая параллельна оси абсцисс.
b
является показателем ординаты точки
пересечения прямой с осью ординат.
При ![]() ,
прямая проходит через начало координат.
,
прямая проходит через начало координат.



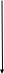


Y=kx+b, k<0
Y=kx+b, k>0
Степенна́я
фу́нкция — функция ![]() ,
где
,
где ![]() (показатель
степени) —
некоторое вещественное
число.
К степенным часто относят и функцию
вида
(показатель
степени) —
некоторое вещественное
число.
К степенным часто относят и функцию
вида ![]() ,
гдеk —
некоторый масштабный множитель.
,
гдеk —
некоторый масштабный множитель.
Область определения
Если
показатель степени — целое
число,
то можно рассматривать степенную функцию
на всей числовой
прямой (кроме,
возможно, нуля). В общем случае степенная
функция определена при ![]() .
Если
.
Если ![]() ,
то функция определена также и при
,
то функция определена также и при ![]() ,
иначе нуль является её особой точкой.
,
иначе нуль является её особой точкой.
Рациональный показатель степени
Графики
степенной функции
при натуральном показателе n называются параболами порядка
n.
При ![]() получается
функция
получается
функция ![]() ,
называемая прямой
пропорциональной зависимостью.
,
называемая прямой
пропорциональной зависимостью.
Графики
функций вида ![]() ,
где n —
натуральное число, называются гиперболами порядка
n.
При
,
где n —
натуральное число, называются гиперболами порядка
n.
При ![]() получается
функция
получается
функция ![]() ,
называемая обратной
пропорциональной зависимостью.
,
называемая обратной
пропорциональной зависимостью.
Графики
степенных функций:


 1)y=x2n
2)y=x2n+1
3)y=x-n
1)y=x2n
2)y=x2n+1
3)y=x-n
Билет№7. Градиент функции двух переменных и его свойства.
Градиент функции – это вектор, координаты которого являются частными производными этой функции.
Z=f(x;y) градиент Z={z’x;z’y}
U=f(x1; x2…; xn) gradU=(u’ x1 ; u’ x2…;u’ xn)
Свойства градиента:
Градиент показывает направление максимального возрастания функции.
В каждой точке области определения градиент перпендикулярен линии уровня, проходящей через эту точку(то есть касательной к линии уровня)
Производная по направлению вектора, перпендикулярного к вектору gradu, равна нулю.
Пример: Z= √x^2 +y^2
Z’x = x/ √ x^2 +y^2 Z’y = y/ √x^2 +y^2 gradZ={ x/ √ x^2 +y^2 ; y/ √x^2 +y^2}
 C=
√x^2
+y^2
C=
√x^2
+y^2
Билет №8.
Показательная ф-ция – одна из основных элементарных ф-ций, имеет вид y=ax , а>0, а(не)=0.
Свойства: 1) а0 =1; 2)ax+y =axay ; 3)(ax)y=axy; 4)(ab)x=axbx
Используя функцию натурального логарифма lnx, можно выразить показательную функцию с произвольным положительным основанием через экспоненту: ax=ex*lna
Для
а>1:
 для 0<a<1:
для 0<a<1:

Билет №9.
Логарифмическая
ф-ция
- одна из основных элементарных ф-ций,
имеет вид y=logax,
a>0,
a(не)=1.Св-ва:
1)основное логарифм.тождество:
![]() ;
2) Логарифмы
единицы и числа, равного основанию:
loga1=0;
logaa=1;
3)
Логарифм
произведения, частного от деления,
степени и корня: loga(xy)=logax+logay;
;
2) Логарифмы
единицы и числа, равного основанию:
loga1=0;
logaa=1;
3)
Логарифм
произведения, частного от деления,
степени и корня: loga(xy)=logax+logay;
![]() ;
;
![]() ;
4) Замена основания логарифма:
;
4) Замена основания логарифма:
![]() ;
;
![]() .
.

Билет №10. Числовые последовательности и способы их задания. Примеры.
Последовательностью называется числовая функция fn, заданная на множестве натуральных чисел N.
Обозначается через an, (an), {an}. Если n - натуральное число, а an - значение последовательности в тоске n, то n - номер числа a, а само число an - общий или n-ый член последовательности.
График - изолированное множество точек плоскости.
Способы задания числовых последовательностей:
1) формулой
n-го члена.
1,
4, 9, 16, 25, 36, ... …
2) описания
членов
2,
4, 6, 8, 10, ...
…
2) описания
членов
2,
4, 6, 8, 10, ...
 ...
1,
3, 5, 7, 9, ...
...
1,
3, 5, 7, 9, ...
 ...
3) рекуррентным
1,
1, 2, 3, 5, 8, 13, 21, ...
an
=
an-1
+
an-2
,
...
3) рекуррентным
1,
1, 2, 3, 5, 8, 13, 21, ...
an
=
an-1
+
an-2
,
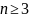 …
…
Пример.
Последовательность Фибоначчи.
Проблема с кроликами: человек пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Ряд, каждый член в котором - сумма двух предыдущих.
Билет №11. Определение предела числовой последовательности. Пример.
Число a называется
пределом числовой
последовательности {an},
если для любого, сколь угодно малого
положительного числа эпсилон>0,
найдется такое число N (зависящее от
эпсилон, N=Nԑ),
что для всех членов последовательности
с номерами n>N верно неравенство
 эпсилон.
эпсилон.
Если
это выполняется, то пишут
 или
или
 при n
при n ∞
∞
Последовательность может быть сходящаяся/расходящаяся.
Используя логические символы определение

Смысл определения: для достаточно больших n члены последовательности {an} как угодно мало отличаются от числа a (по абсолютной величине меньше, чем на число ԑ, каким бы малым оно ни было).
Пример.
 С
ростом номера n число an
становится все ближе к 1.
С
ростом номера n число an
становится все ближе к 1.

Билет №12. Отрицание определения предела последовательности. Пример последовательности не имеющей предела.


Построение отрицаний
Х,У- люди
 х любит у
х любит у
Отрицает
 х
х у
х не любит у
у
х не любит у


Предела lim sin x не существует
Хотелось бы, чтобы вы почувствовали, что это так. Чтобы предел существовал, надо, чтобы при стремлении х → +бесконечность
значения sin x приближались к какому-то конечному значению, либо стремились бы к бесконечности. А тут значения sin x колеблются между –1 и +1, не имея тенденции приближаться к какому-нибудь числу.
Билет №13. Бесконечно малые и бесконечно большие последовательности и их свойства.

Свойства бесконечно малых и бесконечно больших последовательностей
Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Любая бесконечно малая последовательность ограничена.
Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.
Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.
Если — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно малой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно малой.
Если — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно большой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно большой.
