Приведение к резистивной форме моделей электрических цепей с одним накопителем энергии.

1. Постановка задачи:

Упрощение электрической цепи путем привидения её к резистивной форме.

2. Текст программы:

>> R=0.628; L=0.1; w=314;E=230;

>> ksi=atan(w*L/R);

>> fi=15;

>> fi1=(pi/180)*fi;

>> t=0:0.0002:0/12;

>> t=0:0.0002:0.12;

>> e=E*cos(w*t+fi1);

>> I=E/(sqrt(R^2+(w*L)^2));

>> bet=fi1-ksi;

>> i1=I*cos(w*t+bet);

>> i2=I*(exp(-R/L*t)).*cos(bet);

>> i=i1-i2;

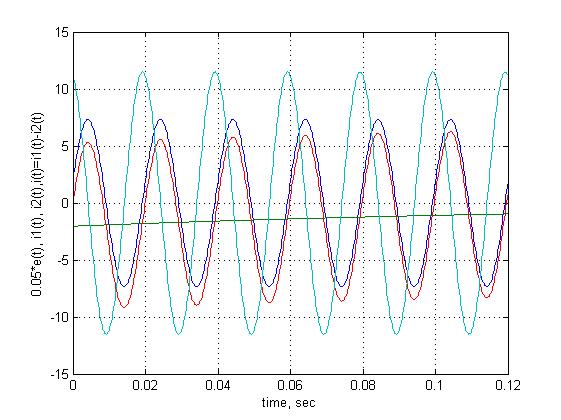
>> plot(t,i1,t,-i2,t,i,t,e*0.05), grid

>> xlabel('time, sec'),

>> ylabel('0.05*e(t), i1(t), i2(t),i(t)=i1(t)-i2(t)')

>> plot(t,i1,t,-i2,t,i,t,e*0.05), grid

>> xlabel('time, sec'),ylabel('0.05*e(t), i1(t), i2(t),i(t)=i1(t)-i2(t)')

Моделирование rlc-цепи.

1. Постановка задачи :

Использование оператора ode45 при моделировании цепи.

2. Текст программы:

>> global a11 a12 a21 a22 b1 b2 E

>> E=100; L=0.001; C=10.0e-06; R1=20; R2=15; R3=5; R4=2;

>> Uc0=R4/(R1+R4)*E; iL0=E/(R1+R4);

>> a11=-(R1+R2+R3)/L; a12=-1/L; a21=1/C; a22=0; b1=1/L; b2=0;

>> t0=0;

>> tf=2.5e-03;

>> x0=[iL0 Uc0]';

>> [t,x]=ode45('sah500',[t0 tf],x0);

>> plot(t,x(:,1),t,x(:,2)*0.05),grid

>> xlabel('time (s)'),

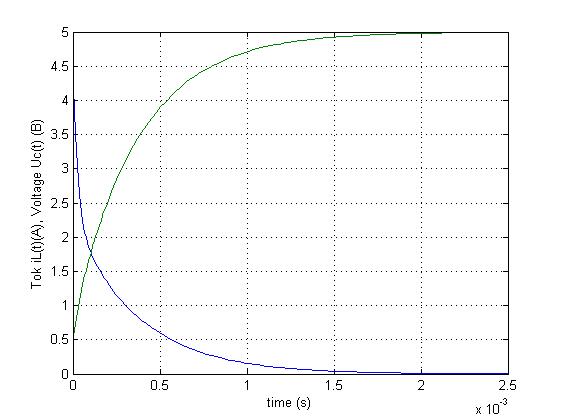
>> plot(t,x(:,1),t,x(:,2)*0.05),grid

>> xlabel('time (s)'),

>> ylabel('Tok iL(t)(A), Напряжение Uc(t) (B)')

>> ylabel('Tok iL(t)(A), Voltage Uc(t) (B)')

>> title('Numerical period')

>> pause

>> A1=[a11 a12;a21 a22]; B1=[b1 b2]'; C1=[1 0;0 1]; D1=[0 0]';

>> eig(A1)

ans =

1.0e+004 *

-3.7321

-0.2679

>> sys1=ss(A1,B1,C1,D1);

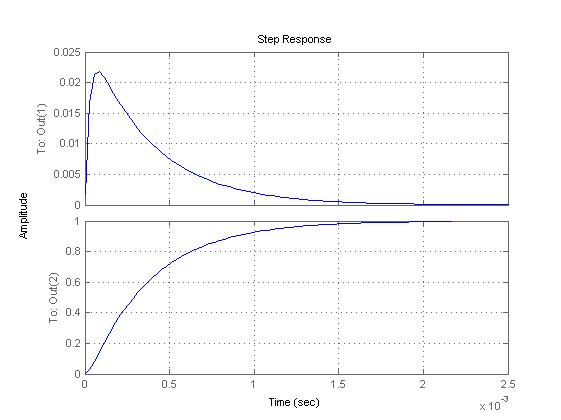
>> step(sys1),grid

>> pause

>> w=50*1/tf;

>> t1=0:tf/500:tf;

>> v=size(t1);

>> u=E*ones(1,v(2));

>> [y,t1,x1]=lsim(sys1,u,t1,x0);

>> [t1,x1];

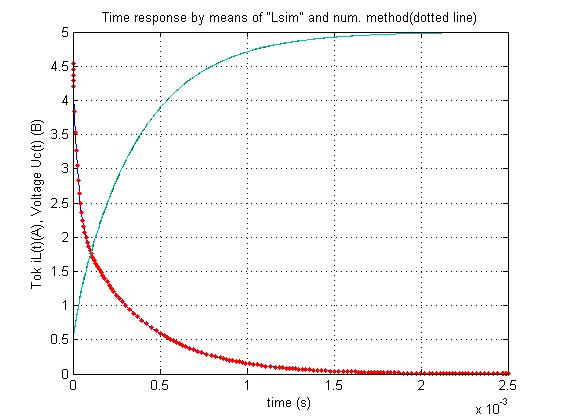
>> plot(t1,y(:,1),t1,y(:,2)*0.05,t,x(:,1),'.',t,x(:,2)*0.05.'.'),grid

>> xlabel('time (s)'),

>> ylabel('Tok iL(t)(A), Voltage Uc(t) (B)')

>> title('Time response by means of "Lsim" and num. method(dotted line)')

>> pause

>> FA=[]; FB=[];

>> for i=0:250;

tau=[0:250;0:250].*tf/250;

Z=expm(A1.*tf/250);

j=Z^i*x0;

FA=[FA j];

J=-(eye(2)-Z^i)*inv(A1)*B1.*E;

FB=[FB J];

end

>> FA;

>> FB;

>> xa=FA+FB;

>> tau1=[0:250]*tf/250;

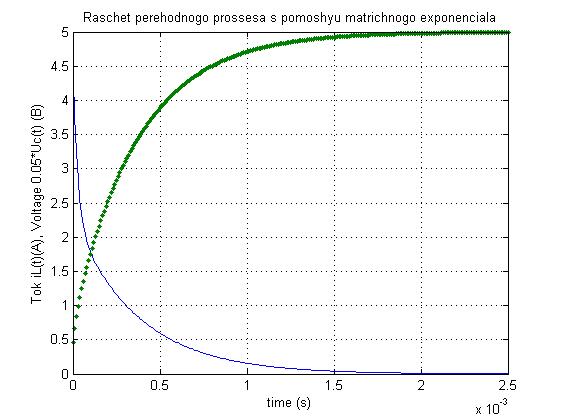
>> plot(tau1,xa(1,:),tau1,xa(2,:)*0.05,'.'),grid

>> xlabel('time (s)'),

>> ylabel('Tok iL(t)(A), Voltage 0.05*Uc(t) (B)')

>> title('Raschet perehodnogo prossesa s pomoshyu matrichnogo exponenciala')

>> pause

>> syms x y s

>> Z=solve(s*x-a11*x-a12*y-b1*E/s-x0(1),-a21*x+s*y-a22*y-b2*E/s-x0(2));

>> I=Z.x;

>> U=Z.y;

>> I=ilaplace(I)

I =

25/11*exp(-10000*(2+3^(1/2))*t)+25/11*exp(10000*(3^(1/2)-2)*t)

>> U=ilaplace(U)

U =

100+100/11*exp(-20000*t)*(-10*cosh(10000*t*3^(1/2))-5*3^(1/2)*sinh(10000*t*3^(1/2)))

>> tt=0:tf/250:tf;

>> x3=subs(I,'t',tt);

>> x4=subs(U,'t',tt);

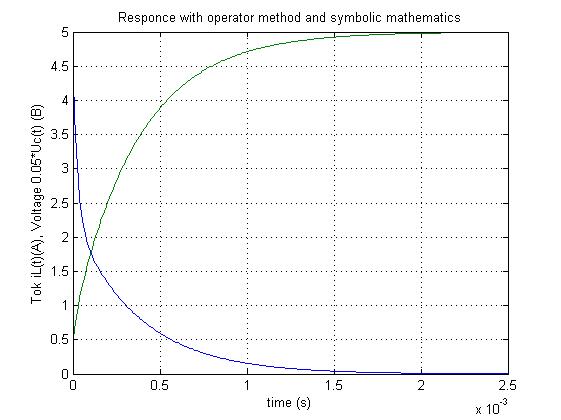
>> plot(tt,x3,tt,x4*0.05),grid

>> xlabel('time (s)'),

>> ylabel('Tok iL(t)(A), Voltage 0.05*Uc(t) (B)')

>> title('Responce with operator method and symbolic mathematics')

Расчет переходного процесса в rlc- цепи с помощью функции initial.

1. Постановка задачи:

Использование функции initial для расчета RLC – цепи.